METODE PENYELESAIAN PERTIMBANGAN TRIGONOMETRI
Relevansi. Secara historis, persamaan dan pertidaksamaan trigonometri mendapat perhatian paling besar. tempat spesial V kursus sekolah. Kita dapat mengatakan bahwa trigonometri adalah salah satu bagian terpenting dari kursus sekolah dan keseluruhannya ilmu matematika umumnya.
Persamaan dan pertidaksamaan trigonometri menempati salah satu tempat-tempat sentral dalam suatu mata pelajaran matematika sekolah menengah, baik dari segi isi materi pendidikan maupun dari segi metode kegiatan pendidikan dan kognitif yang dapat dan harus dibentuk selama pembelajarannya dan diterapkan pada penyelesaiannya jumlah besar masalah yang bersifat teoritis dan terapan.
Larutan persamaan trigonometri dan kesenjangan menciptakan prasyarat untuk mensistematisasikan pengetahuan siswa terkait segala hal materi pendidikan dalam trigonometri (misalnya sifat-sifat fungsi trigonometri, metode transformasi ekspresi trigonometri, dll.) dan memungkinkan terjalinnya hubungan yang efektif dengan materi yang dipelajari dalam aljabar (persamaan, persamaan persamaan, pertidaksamaan, transformasi identitas ekspresi aljabar dll.).
Dengan kata lain, pertimbangan teknik untuk menyelesaikan persamaan dan pertidaksamaan trigonometri melibatkan semacam transfer keterampilan ini ke konten baru.
Pentingnya teori dan banyaknya penerapannya merupakan bukti relevansi topik yang dipilih. Hal ini pada gilirannya memungkinkan Anda untuk menentukan tujuan, sasaran dan subjek penelitian dari tugas kursus.
Tujuan penelitian: menggeneralisasi jenis-jenis pertidaksamaan trigonometri yang ada, metode dasar dan khusus untuk menyelesaikannya, memilih serangkaian masalah untuk menyelesaikan pertidaksamaan trigonometri oleh anak sekolah.
Tujuan penelitian:
1. Berdasarkan analisis literatur yang tersedia tentang topik penelitian, sistematiskan materinya.
2. Memberikan serangkaian tugas yang diperlukan untuk mengkonsolidasikan topik “Pertidaksamaan trigonometri.”
Objek studi adalah pertidaksamaan trigonometri dalam mata pelajaran matematika sekolah.
Subyek studi: jenis pertidaksamaan trigonometri dan cara penyelesaiannya.
Signifikansi teoretis adalah mensistematisasikan materi.
Signifikansi praktis: penerapan pengetahuan teoritis dalam memecahkan masalah; analisis metode umum utama untuk menyelesaikan pertidaksamaan trigonometri.
Metode penelitian : analisis literatur ilmiah, sintesis dan generalisasi pengetahuan yang diperoleh, analisis pemecahan masalah, pencarian metode optimal untuk menyelesaikan kesenjangan.
§1. Jenis-jenis pertidaksamaan trigonometri dan cara dasar penyelesaiannya
1.1. Pertidaksamaan trigonometri paling sederhana
Dua ekspresi trigonometri, dihubungkan dengan tanda atau >, disebut pertidaksamaan trigonometri.
Menyelesaikan pertidaksamaan trigonometri berarti mencari himpunan nilai-nilai yang tidak diketahui yang termasuk dalam pertidaksamaan yang memenuhi pertidaksamaan tersebut.
Bagian utama dari pertidaksamaan trigonometri diselesaikan dengan mereduksinya menjadi solusi paling sederhana:
Ini mungkin metode faktorisasi, perubahan variabel ( 
, 
dll.), di mana pertidaksamaan biasa diselesaikan terlebih dahulu, dan kemudian pertidaksamaan berbentuk 
dll., atau metode lain.
Pertidaksamaan yang paling sederhana dapat diselesaikan dengan dua cara: menggunakan lingkaran satuan atau secara grafis.
Membiarkanf(x
– salah satu fungsi trigonometri dasar. Untuk mengatasi ketimpangan 
cukup mencari solusinya dalam satu periode, yaitu. pada setiap segmen yang panjangnya sama dengan periode fungsiF
X
. Maka solusi dari pertidaksamaan awal akan ditemukan semuanyaX
, serta nilai-nilai yang berbeda dari nilai yang ditemukan pada bilangan bulat periode fungsi. Dalam hal ini, akan lebih mudah untuk menggunakan metode grafis.
Mari kita beri contoh algoritma untuk menyelesaikan pertidaksamaan 
(
) Dan 
.
Algoritma untuk menyelesaikan ketimpangan (
).
1. Merumuskan definisi sinus suatu bilanganX pada lingkaran satuan.
3. Pada sumbu ordinat, tandai titik tersebut dengan koordinatA .
4. Melalui titik ini menggambar garis lurus sejajar dengan sumbu OX, dan tandai titik potongnya dengan lingkaran.
5. Pilih busur lingkaran yang semua titiknya mempunyai ordinat kurang dariA .
6. Tunjukkan arah putaran (berlawanan arah jarum jam) dan tuliskan jawabannya dengan menambahkan periode fungsi ke ujung interval2πn
,
.
Algoritma untuk menyelesaikan ketimpangan .
1. Merumuskan definisi garis singgung suatu bilanganX pada lingkaran satuan.
2. Gambarlah lingkaran satuan.
3. Gambarlah garis singgung dan tandai sebuah titik dengan ordinat di atasnyaA .
4. Hubungkan titik ini dengan titik asal dan tandai titik potong segmen yang dihasilkan dengan lingkaran satuan.
5. Pilih busur lingkaran yang semua titiknya mempunyai ordinat pada garis singgung kurang dariA .
6. Tunjukkan arah lintasan dan tulis jawabannya dengan memperhatikan domain definisi fungsi, tambahkan titikπn
,
(Nomor di sebelah kiri dalam entri selalu angka yang lebih sedikit, berdiri di sebelah kanan).
Interpretasi grafis dari solusi persamaan sederhana dan rumus untuk menyelesaikan pertidaksamaan pandangan umum ditunjukkan dalam lampiran (Lampiran 1 dan 2).
Contoh 1.
Selesaikan ketimpangan tersebut 
.
Gambarlah garis lurus pada lingkaran satuan 
, yang memotong lingkaran di titik A dan B.
Semua artikamu
pada interval NM lebih besar
, semua titik busur AMB memenuhi pertidaksamaan ini. Di semua sudut rotasi, besar 
, tapi lebih kecil 
,
akan mengambil nilai yang lebih besar
(tetapi tidak lebih dari satu).
Gambar.1
Jadi, penyelesaian pertidaksamaan tersebut adalah semua nilai dalam interval tersebut 
, yaitu 
. Untuk mendapatkan semua solusi pertidaksamaan ini, cukup dengan menjumlahkan ujung-ujung interval ini 
, Di mana 
, yaitu 
,
.
Perhatikan bahwa nilainya 
Dan 
adalah akar persamaannya 
,
itu. 
;
.
Menjawab: 
, .
1.2. Metode grafis
Dalam praktiknya, metode grafis untuk menyelesaikan pertidaksamaan trigonometri seringkali bermanfaat. Mari kita perhatikan inti dari metode ini dengan menggunakan contoh pertidaksamaan 
:
1. Jika argumennya rumit (berbeda dariX ), lalu ganti denganT .
2. Kami membangun menjadi satu bidang koordinat
mainan
grafik fungsi 
Dan 
.
3. Kami menemukannyadua titik potong grafik yang berdekatan, di antaranyagelombang sinusterletaklebih tinggi
lurus . Kami menemukan absis dari titik-titik ini.
4. Tuliskan pertidaksamaan ganda untuk argumen tersebutT , dengan memperhitungkan periode cosinus (T akan berada di antara absis yang ditemukan).
5. Lakukan substitusi terbalik (kembali ke argumen awal) dan nyatakan nilainyaX dari ketimpangan ganda, tulis jawabannya dalam bentuk interval numerik.
Contoh 2. Selesaikan ketimpangan: .
Saat memecahkan kesenjangan metode grafis perlu untuk membuat grafik fungsi seakurat mungkin. Mari kita ubah pertidaksamaan tersebut menjadi bentuk:
Mari kita buat grafik fungsi dalam satu sistem koordinat 
Dan 
(Gbr. 2).
Gambar.2
Grafik fungsi berpotongan di suatu titikA
dengan koordinat 
; 
. Diantara 
titik grafik 
di bawah titik grafik 
. Dan kapan nilai fungsinya sama. Itu sebabnya pada 
.
Menjawab: 
.
1.3. Metode aljabar
Seringkali, pertidaksamaan trigonometri awal dapat direduksi menjadi pertidaksamaan aljabar (rasional atau irasional) melalui substitusi yang dipilih dengan baik. Metode ini melibatkan transformasi pertidaksamaan, memperkenalkan substitusi, atau mengganti variabel.
Mari lihat contoh spesifik penerapan metode ini.
Contoh 3.
Reduksi ke bentuk yang paling sederhana 
.
(Gbr. 3)
Gambar.3
, 
.
Menjawab: 
,
Contoh 4. Selesaikan ketimpangan:
ODZ: 
, 
.
Menggunakan rumus: 
, 
Mari kita tuliskan pertidaksamaan tersebut dalam bentuk: 
.
Atau, percaya 
setelah transformasi sederhana yang kita dapatkan
,
,
.
Menyelesaikan pertidaksamaan terakhir dengan menggunakan metode interval, kita memperoleh:
Gambar.4
, masing-masing 
. Kemudian dari Gambar. 4 mengikuti 
, Di mana 
.
Gambar.5
Menjawab: 
, 
.
1.4. Metode interval
Skema umum menyelesaikan pertidaksamaan trigonometri menggunakan metode interval:
Dengan menggunakan rumus trigonometri menguraikan pd pengali.
Temukan titik diskontinuitas dan nol dari fungsi tersebut dan letakkan pada lingkaran.
Ambil poin apa sajaKE (tetapi tidak ditemukan sebelumnya) dan cari tahu tanda produknya. Jika hasil kali positif, letakkan sebuah titik di luar lingkaran satuan pada sinar yang bersesuaian dengan sudutnya. Jika tidak, letakkan titik tersebut di dalam lingkaran.
Jika intinya bertemu bilangan genap kali, kita menyebutnya titik multiplisitas genap jika angka ganjil kali – titik multiplisitas ganjil. Gambarlah busur sebagai berikut: mulai dari suatu titikKE , jika titik berikutnya mempunyai multiplisitas ganjil, maka busur tersebut memotong lingkaran di titik tersebut, tetapi jika titik tersebut mempunyai multiplisitas genap, maka busur tersebut tidak berpotongan.
Busur di belakang lingkaran adalah interval positif; di dalam lingkaran terdapat ruang negatif.
Contoh 5. Selesaikan ketimpangan
, 
.
Poin dari seri pertama: 
.
Poin dari seri kedua: 
.
Setiap titik muncul beberapa kali ganjil, artinya semua titik mempunyai multiplisitas ganjil.
Mari kita cari tahu tanda produknya di 
: . Mari kita tandai semua titik pada lingkaran satuan (Gbr. 6):
Beras. 6
Menjawab: 
, 
; 
, 
; 
, 
.
Contoh 6 . Selesaikan ketimpangan tersebut.
Larutan:
Mari kita cari angka nol dari ekspresi tersebut .
MenerimaaeM :
,
;
, 
;
, 
;
, 
;
Pada nilai deret lingkaran satuanX
1
diwakili oleh titik-titik 
. SeriX
2
memberikan poin 
. Sebuah seriX
3
kami mendapat dua poin 
. Terakhir, seriX
4
akan mewakili poin 
. Mari kita gambarkan semua titik ini pada lingkaran satuan, yang menunjukkan multiplisitasnya dalam tanda kurung di samping masing-masing titik tersebut.
Biarkan sekarang nomornya 
akan sama. Mari kita membuat perkiraan berdasarkan tandanya:
Jadi, berhenti totalA
harus dipilih pada sinar yang membentuk sudut 
dengan balokOh,
di luar lingkaran satuan. (Perhatikan bahwa balok bantuTENTANG
A
Sama sekali tidak perlu untuk menggambarkannya dalam sebuah gambar. DotA
dipilih kira-kira.)
Sekarang dari intinyaA
gambarlah garis bergelombang terus menerus secara berurutan ke semua titik yang ditandai. Dan pada titik-titik garis kita berpindah dari satu area ke area lain: jika berada di luar lingkaran satuan, maka garis tersebut masuk ke dalamnya. Mendekati intinya 
, garis kembali ke daerah dalam, karena banyaknya titik ini genap. Demikian pula pada intinya 
(dengan multiplisitas genap) garis harus diputar ke daerah terluar. Jadi, kami menggambar gambar tertentu yang ditunjukkan pada Gambar. 7. Membantu menyorot area yang diinginkan pada lingkaran satuan. Mereka ditandai dengan tanda “+”.
Gambar.7
Jawaban akhir:
Catatan. Jika garis bergelombang, setelah melintasi semua titik yang ditandai pada lingkaran satuan, tidak dapat kembali ke titik tersebutA , tanpa melintasi lingkaran di tempat yang “ilegal”, berarti terjadi kesalahan dalam penyelesaiannya, yaitu jumlah akar ganjil yang terlewat.
Menjawab: .
§2. Serangkaian masalah untuk menyelesaikan pertidaksamaan trigonometri
Dalam proses pengembangan kemampuan anak sekolah dalam menyelesaikan pertidaksamaan trigonometri juga dapat dibedakan 3 tahap.
1. persiapan,
2. mengembangkan kemampuan menyelesaikan pertidaksamaan trigonometri sederhana;
3. pengenalan pertidaksamaan trigonometri jenis lain.
Maksud dari tahap persiapan adalah perlunya dikembangkan pada anak sekolah kemampuan menggunakan lingkaran atau grafik trigonometri untuk menyelesaikan pertidaksamaan, yaitu:
Kemampuan menyelesaikan pertidaksamaan sederhana dalam bentuk ,
, ,
,
menggunakan sifat-sifat fungsi sinus dan kosinus;
Kemampuan untuk membangun pertidaksamaan ganda untuk busur lingkaran angka atau untuk busur grafik fungsi;
Kemampuan untuk melakukan berbagai transformasi ekspresi trigonometri.
Tahapan ini disarankan untuk dilaksanakan dalam proses sistematisasi pengetahuan anak sekolah tentang sifat-sifat fungsi trigonometri. Sarana utama dapat berupa tugas-tugas yang ditawarkan kepada siswa dan dilakukan baik di bawah bimbingan seorang guru atau secara mandiri, serta keterampilan yang dikembangkan dalam menyelesaikan persamaan trigonometri.
Berikut adalah contoh tugas tersebut:
1
. Tandai sebuah titik pada lingkaran satuan 
, Jika
.
2.
Di bagian bidang koordinat manakah titik tersebut berada? , Jika 
sama dengan: 
3.
Tandai titik-titik pada lingkaran trigonometri , Jika:
4. Ubah ekspresi menjadi fungsi trigonometriSAYAperempat.
A) 
,
B) 
,
V) 
5. Arc MR diberikan.M - tengahSAYA-kuartal,R - tengahIIkuartal ke-3. Batasi nilai suatu variabelT untuk: (buat pertidaksamaan ganda) a) busur MR; b) busur RM.
6. Tuliskan pertidaksamaan ganda untuk bagian grafik yang dipilih:
Beras. 1
7.
Selesaikan kesenjangan 
, 
, 
, 
.
8. Konversi Ekspresi .
Pada pembelajaran penyelesaian pertidaksamaan trigonometri tahap kedua, kami dapat memberikan rekomendasi berikut terkait metodologi pengorganisasian kegiatan siswa. Dalam hal ini, penting untuk fokus pada keterampilan yang dimiliki siswa untuk dikerjakan lingkaran trigonometri atau grafik yang terbentuk saat menyelesaikan persamaan trigonometri sederhana.
Pertama, memotivasi kelayakan memperoleh penerimaan umum penyelesaian pertidaksamaan trigonometri paling sederhana dapat dicapai dengan mengubah, misalnya, ke pertidaksamaan bentuk 
.
Menggunakan pengetahuan dan keterampilan yang diperoleh di tahap persiapan, siswa akan mereduksi pertidaksamaan yang diajukan ke dalam bentuk 
, namun mungkin akan sulit menemukan serangkaian solusi terhadap ketimpangan yang diakibatkannya, karena Tidak mungkin menyelesaikannya hanya dengan menggunakan sifat-sifat fungsi sinus. Kesulitan ini dapat dihindari dengan mengacu pada ilustrasi yang sesuai (menyelesaikan persamaan secara grafis atau menggunakan lingkaran satuan).
Kedua, guru harus menarik perhatian siswa berbagai cara selesaikan tugas, berikan contoh penyelesaian pertidaksamaan yang tepat baik secara grafis maupun menggunakan lingkaran trigonometri.
Mari kita perhatikan penyelesaian pertidaksamaan berikut ini .
1. Menyelesaikan pertidaksamaan dengan menggunakan lingkaran satuan.
Pada pelajaran pertama tentang menyelesaikan pertidaksamaan trigonometri, kami akan menawarkan kepada siswa algoritma penyelesaian yang terperinci, yang dalam presentasi langkah demi langkah mencerminkan semua keterampilan dasar yang diperlukan untuk menyelesaikan pertidaksamaan tersebut.
Langkah 1.Mari kita menggambar lingkaran satuan dan menandai sebuah titik pada sumbu ordinat 
dan tarik garis lurus melaluinya sejajar dengan sumbu x. Garis ini akan memotong lingkaran satuan di dua titik. Masing-masing titik ini mewakili bilangan yang sinusnya sama .
Langkah 2.Garis lurus ini membagi lingkaran menjadi dua busur. Mari kita pilih salah satu yang menggambarkan bilangan yang memiliki sinus lebih besar dari . Secara alami, busur ini terletak di atas garis lurus yang ditarik.
Beras. 2
Langkah 3.Pilih salah satu ujung busur yang ditandai. Mari kita tuliskan salah satu bilangan yang diwakili oleh titik lingkaran satuan ini 
.
Langkah 4.Untuk memilih nomor yang sesuai dengan ujung kedua dari busur yang dipilih, kita “berjalan” di sepanjang busur ini dari ujung yang disebutkan ke ujung lainnya. Pada saat yang sama, ingatlah bahwa ketika bergerak berlawanan arah jarum jam, angka yang akan kita lalui bertambah (bila bergerak berlawanan arah, angka tersebut akan berkurang). Mari kita tuliskan bilangan yang digambarkan pada lingkaran satuan di ujung kedua busur yang ditandai 
.
Jadi, kita melihat ketimpangan itu memenuhi bilangan-bilangan yang pertidaksamaannya benar 
. Kami menyelesaikan pertidaksamaan bilangan-bilangan yang terletak pada periode yang sama dengan fungsi sinus. Oleh karena itu, semua penyelesaian pertidaksamaan dapat dituliskan dalam bentuk 
Siswa harus diminta untuk hati-hati memeriksa gambar tersebut dan mencari tahu mengapa semua solusi terhadap pertidaksamaan tersebut dapat ditulis dalam bentuk 
, 
.
Beras. 3
Penting untuk menarik perhatian siswa pada fakta bahwa ketika menyelesaikan pertidaksamaan fungsi kosinus, kita menggambar garis lurus yang sejajar dengan sumbu ordinat.
Metode grafis solusi terhadap kesenjangan.
Kami membuat grafik 
Dan 
, mengingat bahwa 
.
Beras. 4
Lalu kita menulis persamaannya 
dan keputusannya 
, 
, 
, ditemukan menggunakan rumus 
, 
, 
.
(MemberiN
nilai 0, 1, 2, kita cari ketiga akar persamaan yang dikompilasi). Nilai-nilai 
adalah tiga absis berurutan dari titik potong grafik Dan . Yang jelas, selalu pada interval 
ketimpangan tetap terjadi 
, dan pada intervalnya 
– ketimpangan 
. Kami tertarik pada kasus pertama, dan kemudian menambahkan ke ujung interval ini bilangan yang merupakan kelipatan periode sinus, kami memperoleh solusi untuk pertidaksamaan tersebut. sebagai: 
, .
Beras. 5
Meringkaskan. Untuk mengatasi ketimpangan , kamu perlu membuatnya persamaan yang sesuai dan menyelesaikannya. Temukan akar dari rumus yang dihasilkan 
Dan 
, dan tuliskan jawaban pertidaksamaan tersebut dalam bentuk: , .
Ketiga, fakta tentang himpunan akar-akar yang bersesuaian pertidaksamaan trigonometri Ini dikonfirmasi dengan sangat jelas ketika menyelesaikannya secara grafis.
Beras. 6
Penting untuk menunjukkan kepada siswa bahwa belokan yang merupakan penyelesaian pertidaksamaan berulang setelah selang waktu yang sama, sama dengan periode fungsi trigonometri. Anda juga dapat mempertimbangkan ilustrasi serupa untuk grafik fungsi sinus.
Keempat, disarankan untuk melakukan upaya memperbarui teknik siswa untuk mengubah jumlah (selisih) fungsi trigonometri menjadi produk, dan menarik perhatian siswa pada peran teknik ini dalam menyelesaikan pertidaksamaan trigonometri.
Pekerjaan ini dapat diatur melalui eksekusi sendiri siswa dari tugas-tugas yang diajukan oleh guru, di antaranya kami soroti sebagai berikut:
Kelima, siswa diminta untuk mengilustrasikan penyelesaian setiap pertidaksamaan trigonometri sederhana dengan menggunakan grafik atau lingkaran trigonometri. Anda pasti harus memperhatikan kegunaannya, terutama penggunaan lingkaran, karena ketika menyelesaikan pertidaksamaan trigonometri, ilustrasi yang sesuai berfungsi sebagai cara yang sangat mudah untuk mencatat himpunan solusi pertidaksamaan tertentu.
Disarankan untuk memperkenalkan siswa pada metode penyelesaian pertidaksamaan trigonometri yang bukan yang paling sederhana sesuai dengan skema berikut: mengatasi pertidaksamaan trigonometri tertentu mengatasi persamaan trigonometri yang bersesuaian pencarian bersama(guru – siswa) dalam mengambil keputusan, secara mandiri mentransfer metode yang ditemukan ke pertidaksamaan lain yang sejenis.
Untuk mensistematisasikan pengetahuan siswa tentang trigonometri, sebaiknya pilih secara khusus pertidaksamaan tersebut, yang penyelesaiannya memerlukan berbagai transformasi yang dapat dilaksanakan dalam proses penyelesaiannya, dan memusatkan perhatian siswa pada ciri-cirinya.
Sebagai contoh kesenjangan produktif, kami dapat mengusulkan hal-hal berikut:
Sebagai kesimpulan, kami memberikan contoh himpunan masalah untuk menyelesaikan pertidaksamaan trigonometri.
1. Selesaikan pertidaksamaan:
2. Selesaikan pertidaksamaan: 3. Temukan semua solusi atas ketidaksetaraan: 4. Temukan semua solusi atas ketidaksetaraan:A) 
, memenuhi kondisi 
;
B) 
, memenuhi kondisi 
.
5. Temukan semua solusi atas ketidaksetaraan:
A) ;
B) ;
V) 
;
G) 
;
D) 
.
6. Selesaikan pertidaksamaan:
A) ;
B) ;
V) ;
G) 
;
D) ;
e) ;
Dan) 
.
7. Selesaikan pertidaksamaan:
A) 
;
B) ;
V) ;
G) .
8. Selesaikan pertidaksamaan:
A) ;
B) ;
V) ;
G) 
;
D) 
;
e) ;
Dan) 
;
H) .
Dianjurkan untuk menawarkan tugas 6 dan 7 kepada siswa yang belajar matematika di tingkat tinggi, tugas 8 – untuk siswa kelas dengan studi matematika tingkat lanjut.
§3. Metode khusus penyelesaian pertidaksamaan trigonometri
Metode khusus untuk menyelesaikan persamaan trigonometri - yaitu metode yang hanya dapat digunakan untuk menyelesaikan persamaan trigonometri. Metode ini didasarkan pada penggunaan sifat-sifat fungsi trigonometri, serta penggunaan berbagai rumus dan identitas trigonometri.
3.1. Metode sektor
Mari kita pertimbangkan metode sektor untuk menyelesaikan pertidaksamaan trigonometri. Memecahkan pertidaksamaan bentuk 
, Di manaP
(
X
)
DanQ
(
X
)
– fungsi trigonometri rasional (sinus, cosinus, garis singgung dan kotangen termasuk di dalamnya secara rasional), mirip dengan penyelesaian pertidaksamaan rasional. Ketimpangan rasional Lebih mudah untuk menyelesaikannya menggunakan metode interval pada garis bilangan. Analoginya untuk menyelesaikan pertidaksamaan trigonometri rasional adalah metode sektor-sektor dalam lingkaran trigonometri, misalnyadosa
Dankarena
(
) atau setengah lingkaran trigonometri untuktgx
Danctgx
(
).
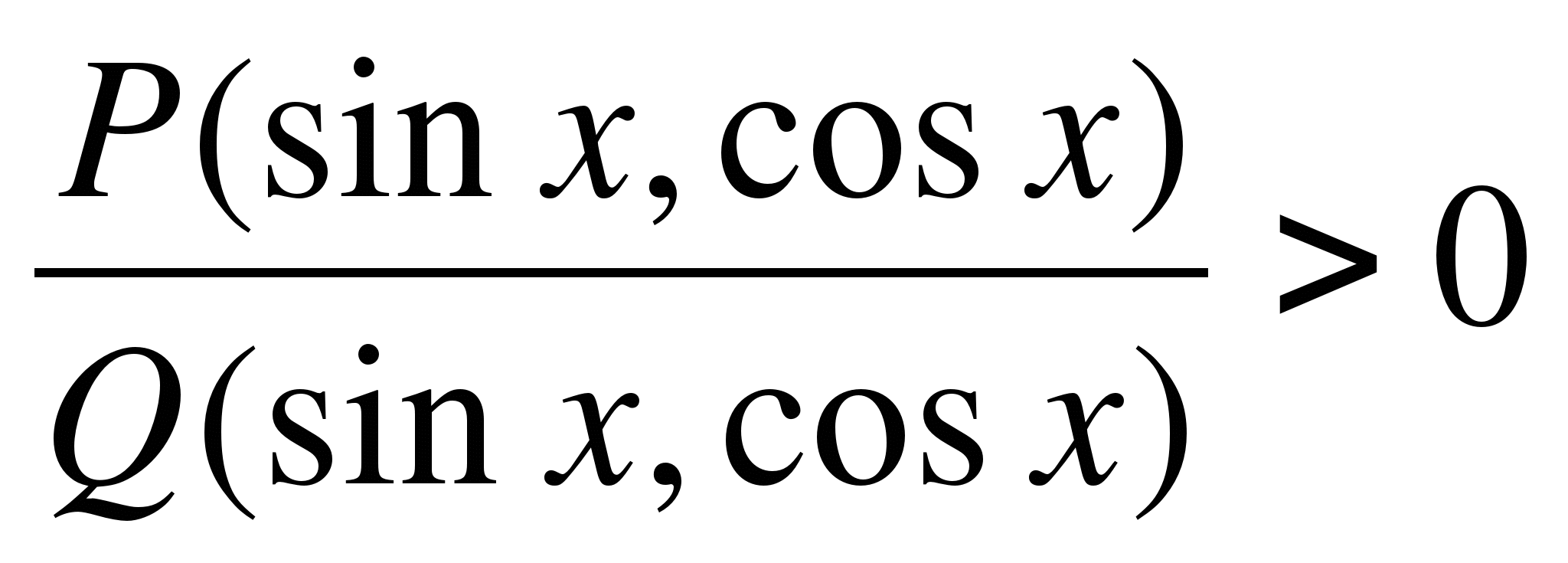
Pada metode interval, setiap faktor linier berbentuk pembilang dan penyebut 
pada sumbu bilangan berhubungan dengan suatu titik 
, dan ketika melewati titik ini tanda perubahan. Dalam metode sektor, setiap faktor berbentuk 
, Di mana 
- salah satu fungsinyadosa
ataukarena
Dan 
, dalam lingkaran trigonometri terdapat dua sudut yang bersesuaian 
Dan 
, yang membagi lingkaran menjadi dua sektor. Saat melewati Dan fungsi tanda perubahan.
Hal-hal berikut harus diingat:
a) Faktor bentuk 
Dan 
, Di mana 
, pertahankan tanda untuk semua nilai 
. Faktor pembilang dan penyebut tersebut dibuang dengan mengubah (jika 
) dengan setiap penolakan tersebut, tanda pertidaksamaan dibalik.
b) Faktor bentuk 
Dan 
juga dibuang. Selain itu, jika ini adalah faktor penyebutnya, maka pertidaksamaan bentuk tersebut ditambahkan ke sistem pertidaksamaan yang ekuivalen. 
Dan 
. Jika ini adalah faktor pembilangnya, maka masuk sistem yang setara pembatasan-pembatasan tersebut berhubungan dengan kesenjangan Dan dalam kasus ketidaksetaraan awal yang ketat, dan kesetaraan 
Dan 
dalam kasus pertidaksamaan awal yang tidak ketat. Saat membuang pengganda 
atau 
tanda pertidaksamaan dibalik.
Contoh 1.
Memecahkan kesenjangan: a) 
, B) 
.
kami memiliki fungsi b) . Selesaikan ketimpangan yang kita punya,
3.2. Metode lingkaran konsentris
Metode ini analog dengan metode sumbu bilangan paralel untuk menyelesaikan sistem pertidaksamaan rasional.
Mari kita perhatikan contoh sistem ketidaksetaraan.
Contoh 5.
Memecahkan sistem pertidaksamaan trigonometri sederhana 
Pertama, kita selesaikan setiap pertidaksamaan secara terpisah (Gambar 5). Di kanan pojok atas Pada gambar kami akan menunjukkan argumen mana yang dipertimbangkan lingkaran trigonometri.
Gambar.5
Selanjutnya, kita membangun sistem lingkaran konsentris untuk argumen tersebutX . Kita menggambar sebuah lingkaran dan mengarsirnya sesuai dengan penyelesaian pertidaksamaan pertama, kemudian kita menggambar sebuah lingkaran dengan jari-jari yang lebih besar dan mengarsirnya sesuai dengan penyelesaian pertidaksamaan kedua, kemudian kita membuat sebuah lingkaran untuk pertidaksamaan ketiga dan sebuah lingkaran alas. Kita menarik sinar dari pusat sistem melalui ujung-ujung busur sehingga memotong semua lingkaran. Kami membentuk solusi pada lingkaran dasar (Gambar 6).
Gambar.6
Menjawab:
, 
.
Kesimpulan
Semua tugas penelitian kursus telah selesai. Tersistematisasi materi teori: diberikan jenis-jenis utama pertidaksamaan trigonometri dan metode utama penyelesaiannya (grafis, aljabar, metode interval, sektor, dan metode lingkaran konsentris). Contoh penyelesaian pertidaksamaan diberikan untuk setiap metode. Bagian teoritis diikuti oleh bagian praktis. Ini berisi serangkaian tugas untuk menyelesaikan pertidaksamaan trigonometri.
Kursus ini dapat digunakan oleh siswa untuk pekerjaan mandiri. Anak-anak sekolah dapat memeriksa tingkat penguasaan topik ini dan berlatih menyelesaikan tugas-tugas dengan kompleksitas yang berbeda-beda.
Setelah mempelajari literatur yang relevan tentang masalah ini Jelasnya, kita dapat menyimpulkan bahwa kemampuan dan keterampilan menyelesaikan pertidaksamaan trigonometri dalam mata pelajaran aljabar sekolah dan permulaan analisis sangatlah penting, yang pengembangannya memerlukan usaha yang signifikan dari pihak guru matematika.
Itu sebabnya pekerjaan ini akan berguna bagi guru matematika, karena memungkinkan penyelenggaraan pelatihan siswa secara efektif tentang topik “Pertidaksamaan trigonometri.”
Penelitian dapat dilanjutkan dengan mengembangkannya menjadi karya kualifikasi akhir.
Daftar literatur bekas
Bogomolov, N.V. Kumpulan Soal Matematika [Teks] / N.V. Bogomolov. – M.: Bustard, 2009. – 206 hal.
Vygodsky, M.Ya. Buku Pegangan Matematika Dasar [Teks] / M.Ya. Vygodsky. – M.: Bustard, 2006. – 509 hal.
Zhurbenko, L.N. Matematika dalam contoh dan soal [Teks] / L.N. Zhurbenko. – M.: Infra-M, 2009. – 373 hal.
Ivanov, O.A. Matematika dasar untuk anak sekolah, siswa dan guru [Teks] / O.A. Ivanov. – M.: MTsNMO, 2009. – 384 hal.
Karp, A.P. Tugas aljabar dan analisis permulaan untuk penyelenggaraan pengulangan akhir dan sertifikasi di kelas 11 [Teks] / A.P. Karper. – M.: Pendidikan, 2005. – 79 hal.
Kulanin, E.D. 3000 soal kompetisi matematika [Teks] / E.D. Kulanin. – M.: Iris-press, 2007. – 624 hal.
Leibson, K.L. Koleksi tugas-tugas praktis dalam matematika [Teks] / K.L. Leibson. – M.: Bustard, 2010. – 182 hal.
Siku, V.V. Masalah dengan parameter dan solusinya. Trigonometri: persamaan, pertidaksamaan, sistem. kelas 10 [Teks] / V.V. Siku. – M.: ARKTI, 2008. – 64 hal.
Manova, A.N. Matematika. Tutor ekspres untuk persiapan Ujian Negara Bersatu: siswa. manual [Teks] / A.N. Manova. –Rostov-on-Don: Phoenix, 2012. – 541 hal.
Mordkovich, A.G. Aljabar dan permulaan analisis matematis. kelas 10-11. Buku teks untuk siswa lembaga pendidikan[Teks] / A.G. Mordkovich. – M.: Iris-press, 2009. – 201 hal.
Novikov, A.I. Fungsi trigonometri, persamaan dan pertidaksamaan [Teks] / A.I. Novikov. – M.: FIZMATLIT, 2010. – 260 hal.
Oganesyan, V.A. Metode pengajaran matematika di sekolah menengah atas: Metodologi umum. Buku pelajaran manual untuk siswa fisika - tikar. palsu. ped. Inst. [Teks] / V.A. Oganesyan. – M.: Pendidikan, 2006. – 368 hal.
Olehnik, S.N. Persamaan dan pertidaksamaan. Metode non-standar solusi [Teks] / S.N. olehnik. – M.: Rumah Penerbitan Faktorial, 1997. – 219 hal.
Sevryukov, P.F. Trigonometri, eksponensial dan persamaan logaritma dan ketidaksetaraan [Teks] / P.F. Sevryukov. – M.: Pendidikan Masyarakat, 2008. – 352 hal.
Sergeev, I.N. Ujian Negara Bersatu: 1000 soal dengan jawaban dan solusi dalam matematika. Semua tugas grup C [Teks] / I.N. Sergeev. – M.: Ujian, 2012. – 301 hal.
Sobolev, A.B. Matematika dasar [Teks] / A.B. Sobolev. – Ekaterinburg: Lembaga Pendidikan Tinggi Negeri USTU-UPI, 2005. – 81 hal.
Fenko, L.M. Metode interval dalam menyelesaikan pertidaksamaan dan mempelajari fungsi [Teks] / L.M. Fenko. – M.: Bustard, 2005. – 124 hal.
Friedman, L.M. Landasan teori metode pengajaran matematika [Teks] / L.M. Friedman. - M.: Rumah Buku“LIBROKOM”, 2009. – 248 hal.
Lampiran 1
Interpretasi grafis dari solusi ketidaksetaraan sederhana
Beras. 1
Beras. 2
Gambar.3
Gambar.4
Gambar.5
Gambar.6
Gambar.7
Gambar.8
Lampiran 2
Solusi untuk kesenjangan sederhana
1. Jika argumennya rumit (berbeda dari X), lalu ganti dengan T.
2. Kita membangun dalam satu bidang koordinat mainan grafik fungsi y=biaya Dan kamu=a.
3. Kami menemukannya dua titik potong grafik yang berdekatan, di antaranya berada di atas garis lurus y=a. Kami menemukan absis dari titik-titik ini.
4. Tuliskan pertidaksamaan ganda untuk argumen tersebut T, dengan memperhitungkan periode cosinus ( T akan berada di antara absis yang ditemukan).
5. Lakukan substitusi terbalik (kembali ke argumen awal) dan nyatakan nilainya X dari pertidaksamaan ganda tersebut kita tuliskan jawabannya dalam bentuk interval numerik.
Contoh 1.
Selanjutnya, menurut algoritma, kita menentukan nilai argumen tersebut T, di mana sinusoida berada lebih tinggi lurus. Mari kita tulis nilai-nilai ini sebagai pertidaksamaan ganda, dengan mempertimbangkan periodisitas fungsi kosinus, dan kemudian kembali ke argumen awal X.
Contoh 2.
Memilih rentang nilai T, yang sinusoidanya berada di atas garis lurus.
Nilainya kita tuliskan dalam bentuk pertidaksamaan ganda T, memuaskan kondisinya. Jangan lupa periode terkecil dari fungsi tersebut y=biaya sama 2π. Kembali ke variabel X, secara bertahap menyederhanakan semua bagian dari pertidaksamaan ganda.
Kami menulis jawabannya dalam bentuk interval numerik tertutup, karena pertidaksamaannya tidak tegas.
Contoh 3.
Kami akan tertarik pada rentang nilai T, di mana titik-titik sinusoida akan terletak di atas garis lurus.
Nilai-nilai T tuliskan dalam bentuk pertidaksamaan ganda, tulis ulang nilainya yang sama 2x dan mengungkapkan X. Mari kita tuliskan jawabannya dalam bentuk interval numerik.
Dan lagi rumus biaya>a.
Jika biaya>a, (-1≤A≤1), lalu - arccos a + 2πn< t < arccos a + 2πn, nєZ.
Terapkan rumus untuk menyelesaikan pertidaksamaan trigonometri dan Anda akan menghemat waktu dalam ujian ujian.
Dan sekarang rumus
, yang harus Anda gunakan pada UNT atau Unified State Examination saat menyelesaikan pertidaksamaan bentuk trigonometri biaya
Jika biaya , (-1≤A≤1), lalu arccos a + 2πn< t < 2π — arccos a + 2πn, nєZ.
Terapkan rumus ini untuk menyelesaikan pertidaksamaan yang dibahas dalam artikel ini, dan Anda akan mendapatkan jawabannya lebih cepat dan tanpa grafik apa pun!
Dengan mempertimbangkan periodisitas fungsi sinus, kami menulis pertidaksamaan ganda untuk nilai argumen T, memenuhi pertidaksamaan terakhir. Mari kita kembali ke variabel awal. Mari kita transformasikan pertidaksamaan ganda yang dihasilkan dan nyatakan variabelnya X. Mari kita tuliskan jawabannya dalam bentuk interval.
Mari selesaikan pertidaksamaan kedua:
Saat menyelesaikan pertidaksamaan kedua, kita harus mengubah ruas kiri pertidaksamaan ini menggunakan rumus sinus argumen ganda untuk mendapatkan pertidaksamaan berbentuk: sint≥a. Selanjutnya kami mengikuti algoritmanya.
Kami menyelesaikan pertidaksamaan ketiga:
Lulusan dan pelamar yang terhormat! Perlu diingat bahwa metode penyelesaian pertidaksamaan trigonometri, seperti metode grafis yang diberikan di atas dan, mungkin Anda ketahui, metode penyelesaian menggunakan lingkaran trigonometri satuan (lingkaran trigonometri) hanya dapat diterapkan pada tahap pertama mempelajari bagian trigonometri. “Memecahkan persamaan dan pertidaksamaan trigonometri.” Saya rasa Anda akan ingat bahwa Anda pertama kali menyelesaikan persamaan trigonometri paling sederhana menggunakan grafik atau lingkaran. Namun, sekarang Anda tidak akan berpikir untuk menyelesaikan persamaan trigonometri dengan cara ini. Bagaimana Anda mengatasinya? Benar, sesuai rumus. Jadi pertidaksamaan trigonometri harus diselesaikan dengan menggunakan rumus, terutama pada saat pengujian, kapan setiap menit sangat berharga. Jadi, selesaikan ketiga pertidaksamaan pada pelajaran ini dengan menggunakan rumus yang sesuai.
Jika dosa>a, di mana -1≤ A≤1, lalu busursin a + 2πn< t < π — arcsin a + 2πn, tidakZ.
Pelajari rumus!
Dan terakhir: tahukah Anda bahwa matematika itu definisi, aturan dan FORMULA?!
Tentu saja! Dan yang paling penasaran, setelah mempelajari artikel ini dan menonton videonya, berseru: “Betapa panjang dan sulitnya! Apakah ada rumus yang memungkinkan Anda menyelesaikan pertidaksamaan tersebut tanpa grafik atau lingkaran?” Ya, tentu saja ada!
UNTUK MENYELESAIKAN KETIMPANGAN BENTUK: dosa (-1≤A≤1) rumusnya valid:
— π — busursin a + 2πn< t < arcsin a + 2πn, nєZ.
Terapkan pada contoh yang dibahas dan Anda akan mendapatkan jawabannya lebih cepat!
Kesimpulan: PELAJARI FORMULA YA TEMAN!
Halaman 1 dari 1 1
Kebanyakan siswa tidak menyukai pertidaksamaan trigonometri. Namun sia-sia. Seperti yang pernah dikatakan salah satu karakter,
“Kamu hanya tidak tahu cara memasaknya”
Jadi bagaimana cara “memasak” dan bagaimana cara menyampaikan pertidaksamaan dengan sinus, kita akan cari tahu di artikel ini. Kami akan menyelesaikannya dengan cara paling sederhana - menggunakan lingkaran satuan.
Jadi, pertama-tama, kita memerlukan algoritma berikut.
Algoritma untuk menyelesaikan pertidaksamaan dengan sinus:
- pada sumbu sinus kita plot bilangan $a$ dan menggambar garis lurus sejajar sumbu kosinus hingga berpotongan dengan lingkaran;
- titik potong garis tersebut dengan lingkaran akan diarsir jika pertidaksamaannya tidak tegas, dan tidak diarsir jika pertidaksamaannya tegas;
- luas penyelesaian pertidaksamaan terletak di atas garis dan sampai ke lingkaran jika pertidaksamaan itu bertanda “$>$”, dan di bawah garis dan sampai ke lingkaran jika pertidaksamaan itu bertanda “$<$”;
- untuk mencari titik potong, kita selesaikan persamaan trigonometri $\sin(x)=a$, kita peroleh $x=(-1)^(n)\arcsin(a) + \pi n$;
- pengaturan $n=0$, kita menemukan titik persimpangan pertama (terletak di kuartal pertama atau keempat);
- untuk mencari titik kedua, kita lihat ke arah mana kita melewati daerah tersebut hingga titik potong kedua: jika ke arah positif maka kita ambil $n=1$, dan jika ke arah negatif maka $n=- $1;
- sebagai tanggapan, intervalnya dituliskan dari titik potong yang lebih kecil $+ 2\pi n$ ke titik potong yang lebih besar $+ 2\pi n$.
Batasan algoritma
Penting: d algoritma yang diberikan tidak bekerja untuk pertidaksamaan berbentuk $\sin(x) > 1; \ \dosa(x) \geq 1, \ \dosa(x)< -1, \ \sin{x} \leq -1$. В строгом случае эти неравенства не имеют решений, а в нестрогом – решение сводится к решению уравнения $\sin{x} = 1$ или $\sin{x} = -1$.
Kasus khusus saat menyelesaikan pertidaksamaan dengan sinus
Penting juga untuk memperhatikan kasus-kasus berikut, yang jauh lebih mudah untuk diselesaikan secara logis tanpa menggunakan algoritma di atas.
Kasus khusus 1. Selesaikan ketimpangan:
$\sin(x)\leq 1.$
Karena rentang nilai fungsi trigonometri $y=\sin(x)$ tidak lebih besar dari modulo $1$, maka ruas kiri pertidaksamaan apapun$x$ dari domain definisi (dan domain definisi sinus adalah semua bilangan real) tidak lebih dari $1$. Dan, oleh karena itu, dalam jawabannya kita menulis: $x \in R$.
Konsekuensi:
$\sin(x)\geq -1.$
Kasus khusus 2. Selesaikan ketimpangan:
$\dosa(x)< 1.$
Menerapkan alasan yang mirip dengan kasus khusus 1, kita menemukan bahwa ruas kiri pertidaksamaan kurang dari $1$ untuk semua $x \dalam R$, kecuali titik-titik yang merupakan solusi persamaan $\sin(x) = 1$. Memecahkan persamaan ini, kita akan mendapatkan:
$x = (-1)^(n)\arcsin(1)+ \pi n = (-1)^(n)\frac(\pi)(2) + \pi n.$
Oleh karena itu, dalam jawabannya kita menulis: $x \in R \backslash \left\((-1)^(n)\frac(\pi)(2) + \pi n\right\)$.
Konsekuensi: ketimpangan diselesaikan dengan cara yang sama
$\dosa(x) > -1.$
Contoh penyelesaian pertidaksamaan menggunakan algoritma.
Contoh 1: Selesaikan ketimpangan:
$\sin(x) \geq \frac(1)(2).$
- Mari kita tandai koordinat $\frac(1)(2)$ pada sumbu sinus.
- Mari kita menggambar garis lurus yang sejajar dengan sumbu kosinus dan melalui titik ini.
- Mari kita tandai titik persimpangannya. Mereka akan dinaungi karena kesenjangannya tidak terlalu ketat.
- Tanda pertidaksamaannya adalah $\geq$, artinya kita mengecat area di atas garis, yaitu. setengah lingkaran yang lebih kecil.
- Kami menemukan titik persimpangan pertama. Untuk melakukannya, kita mengubah pertidaksamaan menjadi persamaan dan menyelesaikannya: $\sin(x)=\frac(1)(2) \ \Panah Kanan \ x=(-1)^(n)\arcsin(\frac(1 )(2) )+\pi n =(-1)^(n)\frac(\pi)(6) + \pi n$. Kami selanjutnya menetapkan $n=0$ dan menemukan titik persimpangan pertama: $x_(1)=\frac(\pi)(6)$.
- Kami menemukan poin kedua. Luas kita mengarah ke arah positif dari titik pertama, artinya kita menetapkan $n$ sama dengan $1$: $x_(2)=(-1)^(1)\frac(\pi)(6) + \pi \cdot 1 = \ pi – \frac(\pi)(6) = \frac(5\pi)(6)$.
Maka penyelesaiannya akan berbentuk:
$x \dalam \kiri[\frac(\pi)(6) + 2\pi n; \frac(5\pi)(6) + 2 \pi n\kanan], \n \dalam Z.$
Contoh 2: Selesaikan ketimpangan:
$\dosa(x)< -\frac{1}{2}$
Mari kita tandai koordinat $-\frac(1)(2)$ pada sumbu sinus dan menggambar garis lurus yang sejajar dengan sumbu kosinus dan melalui titik ini. Mari kita tandai titik persimpangannya. Mereka tidak akan dinaungi, karena kesenjangannya sangat ketat. Tanda pertidaksamaan $<$, а, значит, закрашиваем область ниже прямой, т.е. меньший полукруг. Неравенство превращаем в равенство и решаем его:
$\sin(x)=-\frac(1)(2)$
$x=(-1)^(n)\arcsin(\left(-\frac(1)(2)\right))+ \pi n =(-1)^(n+1)\frac(\pi )(6) + \pi n$.
Selanjutnya dengan asumsi $n=0$, kita menemukan titik potong pertama: $x_(1)=-\frac(\pi)(6)$. Luas kita mengarah ke arah negatif dari titik pertama, artinya kita menetapkan $n$ sama dengan $-1$: $x_(2)=(-1)^(-1+1)\frac(\pi)( 6) + \pi \cdot (-1) = -\pi + \frac(\pi)(6) = -\frac(5\pi)(6)$.
Jadi, penyelesaian pertidaksamaan ini adalah intervalnya:
$x \in \left(-\frac(5\pi)(6) + 2\pi n; -\frac(\pi)(6) + 2 \pi n\right), \n \in Z.$
Contoh 3: Selesaikan ketimpangan:
$1 – 2\sin(\kiri(\frac(x)(4)+\frac(\pi)(6)\kanan)) \leq 0.$
Contoh ini tidak dapat diselesaikan dengan segera menggunakan suatu algoritma. Pertama, Anda perlu mengubahnya. Kita melakukan persis seperti yang kita lakukan dengan persamaan, tapi jangan lupa tentang tandanya. Membagi atau mengalikan dengan angka negatif akan membalikkannya!
Jadi, mari kita pindahkan segala sesuatu yang tidak mengandung fungsi trigonometri ke ruas kanan. Kita mendapatkan:
$- 2\sin(\kiri(\frac(x)(4)+\frac(\pi)(6)\kanan)) \leq -1.$
Mari kita bagi ruas kiri dan kanan dengan $-2$ (jangan lupa tandanya!). Akan memiliki:
$\sin(\kiri(\frac(x)(4)+\frac(\pi)(6)\kanan)) \geq \frac(1)(2).$
Sekali lagi kita memiliki pertidaksamaan yang tidak dapat diselesaikan dengan menggunakan algoritma. Tapi di sini cukup mengubah variabelnya:
$t=\frac(x)(4)+\frac(\pi)(6).$
Kami memperoleh pertidaksamaan trigonometri yang dapat diselesaikan dengan menggunakan algoritma:
$\sin(t) \geq \frac(1)(2).$
Pertidaksamaan ini diselesaikan pada Contoh 1, jadi mari kita pinjam jawabannya dari sana:
$t \di \kiri[\frac(\pi)(6) + 2\pi n; \frac(5\pi)(6) + 2 \pi n\kanan].$
Namun, keputusan tersebut belum berakhir. Kita perlu kembali ke variabel awal.
$(\frac(x)(4)+\frac(\pi)(6)) \di \kiri[\frac(\pi)(6) + 2\pi n; \frac(5\pi)(6) + 2 \pi n\kanan].$
Mari kita bayangkan interval sebagai suatu sistem:
$\left\(\begin(array)(c) \frac(x)(4)+\frac(\pi)(6) \geq \frac(\pi)(6) + 2\pi n, \\ \frac(x)(4)+\frac(\pi)(6) \leq \frac(5\pi)(6) + 2 \pi n
Di sisi kiri sistem terdapat ekspresi ($\frac(x)(4)+\frac(\pi)(6)$), yang termasuk dalam interval. Batas kiri interval menyebabkan pertidaksamaan pertama, dan batas kanan menyebabkan pertidaksamaan kedua. Selain itu, tanda kurung juga memegang peranan penting: jika tanda kurung berbentuk persegi, maka pertidaksamaannya akan mengecil, dan jika berbentuk bulat, maka pertidaksamaannya akan tegas. tugas kita adalah mendapatkan $x$ dari kiri dalam kedua ketidaksetaraan.
Mari kita pindahkan $\frac(\pi)(6)$ dari sisi kiri ke sisi kanan, kita peroleh:
$\left\(\begin(array)(c) \frac(x)(4) \geq \frac(\pi)(6) + 2\pi n -\frac(\pi)(6), \\ \frac(x)(4) \leq \frac(5\pi)(6) + 2 \pi n – \frac(\pi)(6) \end(array) \kanan.$.
Sederhananya, kita punya:
$\left\(\begin(array)(c) \frac(x)(4) \geq 2\pi n, \\ \frac(x)(4) \leq \frac(2\pi)(3) + 2 \pi n.\end(array) \kanan.$
Mengalikan ruas kiri dan kanan dengan $4$, kita mendapatkan:
$\left\(\begin(array)(c) x \geq 8\pi n, \\ x \leq \frac(8\pi)(3) + 8 \pi n. \end(array) \kanan. $
Merakit sistem ke dalam interval, kita mendapatkan jawabannya:
$x \di \kiri[ 8\pi n; \frac(8\pi)(3) + 8 \pi n\kanan], \n \dalam Z.$
solusi ketimpangan dalam mode on line larutan hampir semua ketimpangan tertentu on line. Matematis kesenjangan secara online untuk menyelesaikan matematika. Temukan dengan cepat solusi ketimpangan dalam mode on line. Situs web www.site memungkinkan Anda menemukan larutan hampir semua diberikan aljabar, trigonometri atau kesenjangan transendental secara online. Ketika mempelajari hampir semua cabang matematika pada tahapan yang berbeda, Anda harus memutuskan kesenjangan secara online. Untuk mendapatkan jawaban segera, dan yang terpenting jawaban akurat, Anda memerlukan sumber daya yang memungkinkan Anda melakukan hal tersebut. Berkat situs www.site menyelesaikan kesenjangan secara online akan memakan waktu beberapa menit. Keuntungan utama www.site saat menyelesaikan matematika kesenjangan secara online- ini adalah kecepatan dan keakuratan respon yang diberikan. Situs ini mampu menyelesaikan masalah apa pun pertidaksamaan aljabar online, pertidaksamaan trigonometri online, kesenjangan transendental secara online, Dan kesenjangan dengan parameter yang tidak diketahui dalam mode on line. Ketimpangan berfungsi sebagai alat matematika yang kuat solusi masalah praktis. Dengan bantuan ketidaksetaraan matematika adalah mungkin untuk mengungkapkan fakta dan hubungan yang mungkin tampak membingungkan dan rumit pada pandangan pertama. Jumlah yang tidak diketahui kesenjangan dapat ditemukan dengan merumuskan masalah pada matematis bahasa dalam bentuk kesenjangan Dan memutuskan menerima tugas dalam mode on line di situs web www.site. Setiap pertidaksamaan aljabar, pertidaksamaan trigonometri atau kesenjangan mengandung teramat fitur yang Anda dapat dengan mudah memutuskan online dan dapatkan jawaban pastinya. Saat mempelajari ilmu pengetahuan alam, mau tidak mau Anda akan menemui kebutuhan solusi terhadap kesenjangan. Dalam hal ini, jawabannya harus akurat dan harus segera diperoleh dalam mode tersebut on line. Oleh karena itu untuk menyelesaikan pertidaksamaan matematika secara online kami merekomendasikan situs www.site, yang akan menjadi kalkulator yang sangat diperlukan untuk Anda menyelesaikan pertidaksamaan aljabar secara online, pertidaksamaan trigonometri online, Dan kesenjangan transendental secara online atau kesenjangan dengan parameter yang tidak diketahui. Untuk masalah praktis menemukan solusi online yang beragam ketidaksetaraan matematika sumber daya www.. Pemecahan kesenjangan secara online sendiri, akan berguna untuk memeriksa jawaban yang diterima menggunakan penyelesaian kesenjangan secara online di situs web www.site. Anda perlu menulis pertidaksamaan dengan benar dan langsung mendapatkannya solusi daring, setelah itu yang tersisa hanyalah membandingkan jawabannya dengan solusi pertidaksamaan Anda. Mengecek jawabannya tidak lebih dari satu menit, itu sudah cukup menyelesaikan kesenjangan secara online dan bandingkan jawabannya. Ini akan membantu Anda menghindari kesalahan dalam keputusan dan perbaiki jawabannya pada waktunya menyelesaikan kesenjangan secara online salah satu aljabar, trigonometri, teramat atau ketidaksamaan dengan parameter yang tidak diketahui.
Selama pelajaran praktis, kami akan mengulangi jenis tugas utama dari topik “Trigonometri”, selain itu menganalisis masalah dengan kompleksitas yang meningkat dan mempertimbangkan contoh penyelesaian berbagai pertidaksamaan trigonometri dan sistemnya.
Pelajaran ini akan membantu Anda mempersiapkan salah satu jenis tugas B5, B7, C1 dan C3.
Mari kita mulai dengan meninjau jenis tugas utama yang kita bahas dalam topik "Trigonometri" dan menyelesaikan beberapa masalah non-standar.
Tugas No.1. Ubah sudut menjadi radian dan derajat: a) ; B) .
a) Mari kita gunakan rumus untuk mengubah derajat menjadi radian
Mari kita gantikan nilai yang ditentukan ke dalamnya.
b) Terapkan rumus untuk mengubah radian menjadi derajat
Mari kita lakukan substitusi 
.
Menjawab. A) ; B) .
Tugas No.2. Hitung: a) ; B) .
a) Karena sudutnya jauh melampaui tabel, kita akan menguranginya dengan mengurangkan periode sinus. Karena Sudut dinyatakan dalam radian, maka kita anggap periodenya sebagai .
b) Dalam hal ini situasinya serupa. Karena sudut dinyatakan dalam derajat, kita anggap periode garis singgungnya sebagai .
Sudut yang dihasilkan, meskipun lebih kecil dari periode, namun lebih besar, artinya tidak lagi mengacu pada bagian utama, melainkan bagian tabel yang diperpanjang. Agar tidak melatih ingatan Anda sekali lagi dengan menghafal tabel nilai trigofungsi yang diperluas, mari kita kurangi lagi periode singgungnya:
Kami memanfaatkan keanehan fungsi tangen.
Menjawab. a) 1; B) .
Tugas No.3. Menghitung 
, Jika .
Mari kita kurangi seluruh ekspresi menjadi garis singgung dengan membagi pembilang dan penyebut pecahan dengan . Pada saat yang sama, kita tidak boleh takut akan hal itu, karena dalam hal ini, nilai tangen tidak akan ada.
Tugas No.4. Sederhanakan ekspresi tersebut.
Ekspresi yang ditentukan diubah menggunakan rumus reduksi. Mereka ditulis dengan menggunakan derajat yang tidak biasa. Ekspresi pertama umumnya mewakili angka. Mari kita sederhanakan semua fungsi trigo satu per satu:
Karena , maka fungsinya berubah menjadi kofungsi, yaitu. ke kotangen, dan sudutnya jatuh ke kuarter kedua, yang garis singgung aslinya bertanda negatif.
Untuk alasan yang sama seperti pada ekspresi sebelumnya, fungsi berubah menjadi kofungsi, yaitu. ke kotangen, dan sudutnya jatuh ke kuarter pertama, yang garis singgung aslinya bertanda positif.
Mari kita gantikan semuanya ke dalam ekspresi yang disederhanakan:
Masalah #5. Sederhanakan ekspresi tersebut.
Mari kita tuliskan garis singgung sudut ganda menggunakan rumus yang sesuai dan sederhanakan persamaannya:
Identitas terakhir adalah salah satu rumus penggantian universal kosinus.
Masalah #6. Menghitung.
Hal utama adalah jangan membuat kesalahan standar dengan tidak memberikan jawaban yang persamaannya dengan . Sifat dasar garis singgung busur tidak dapat digunakan selama ada faktor berbentuk dua di sebelahnya. Untuk menghilangkannya, kita akan menulis ekspresi sesuai dengan rumus tangen sudut ganda, dengan memperlakukan , sebagai argumen biasa.
Sekarang kita dapat menerapkan sifat dasar tangen busur; ingat bahwa tidak ada batasan pada hasil numeriknya.
Soal No.7. Selesaikan persamaannya.
Ketika menyelesaikan persamaan pecahan yang sama dengan nol, selalu dinyatakan bahwa pembilangnya sama dengan nol, tetapi penyebutnya tidak, karena Anda tidak dapat membaginya dengan nol.
Persamaan pertama merupakan kasus khusus dari persamaan paling sederhana yang dapat diselesaikan dengan menggunakan lingkaran trigonometri. Ingat solusi ini sendiri. Pertidaksamaan kedua diselesaikan sebagai persamaan paling sederhana dengan menggunakan rumus umum akar-akar garis singgung, tetapi hanya dengan tanda tidak sama.
Seperti yang bisa kita lihat, satu famili akar mengecualikan famili lain yang memiliki jenis akar yang persis sama dan tidak memenuhi persamaan tersebut. Itu. tidak ada akar.
Menjawab. Tidak ada akar.
Soal No.8. Selesaikan persamaannya.
Mari kita segera perhatikan bahwa kita dapat menghilangkan faktor persekutuannya dan melakukannya:
Persamaan tersebut telah direduksi menjadi salah satu bentuk standar, dimana hasil kali beberapa faktor sama dengan nol. Kita sudah tahu bahwa dalam kasus ini, salah satunya sama dengan nol, atau yang lain, atau yang ketiga. Mari kita tuliskan dalam bentuk himpunan persamaan:
Dua persamaan pertama adalah kasus khusus dari persamaan paling sederhana yang telah kita jumpai berkali-kali dengan persamaan serupa, jadi kami akan segera menunjukkan solusinya. Kami mengurangi persamaan ketiga menjadi satu fungsi menggunakan rumus sinus sudut ganda.
Mari selesaikan persamaan terakhir secara terpisah:
Persamaan ini tidak mempunyai akar, karena nilai sinus tidak bisa melampauinya 
.
Jadi, solusinya hanyalah dua keluarga akar pertama; keduanya dapat digabungkan menjadi satu, yang mudah ditunjukkan pada lingkaran trigonometri:
 |
Ini adalah keluarga dari semua bagian, mis.
Mari kita lanjutkan menyelesaikan pertidaksamaan trigonometri. Pertama, kita akan menganalisis pendekatan penyelesaian contoh tanpa menggunakan rumus solusi umum, tetapi menggunakan lingkaran trigonometri.
Soal No.9. Selesaikan ketimpangan.
Mari kita menggambar garis bantu pada lingkaran trigonometri yang sesuai dengan nilai sinus sama dengan , dan menunjukkan rentang sudut yang memenuhi pertidaksamaan.
 |
Sangat penting untuk memahami dengan tepat bagaimana menunjukkan interval sudut yang dihasilkan, mis. apa awalnya dan apa akhirnya. Awal interval akan menjadi sudut yang sesuai dengan titik yang akan kita masuki di awal interval jika kita bergerak berlawanan arah jarum jam. Dalam kasus kami, ini adalah titik di sebelah kiri, karena bergerak berlawanan arah jarum jam dan melewati titik yang diinginkan, sebaliknya kita meninggalkan rentang sudut yang diperlukan. Oleh karena itu, titik yang tepat akan berhubungan dengan akhir kesenjangan.
Sekarang kita perlu memahami sudut awal dan akhir interval solusi pertidaksamaan kita. Kesalahan umum adalah segera menunjukkan bahwa titik kanan berhubungan dengan sudut, titik kiri dan memberikan jawabannya. Ini tidak benar! Harap dicatat bahwa kami baru saja menunjukkan interval yang sesuai dengan bagian atas lingkaran, meskipun kami tertarik pada bagian bawah, dengan kata lain, kami telah mencampuradukkan awal dan akhir interval solusi yang kami butuhkan.
Agar interval dimulai dari sudut titik kanan dan diakhiri dengan sudut titik kiri, sudut tertentu pertama harus lebih kecil dari sudut kedua. Untuk melakukan ini, kita harus mengukur sudut titik siku-siku dalam arah acuan negatif, yaitu. searah jarum jam dan itu akan sama dengan. Kemudian, mulai bergerak searah jarum jam positif, kita akan sampai ke titik kanan setelah titik kiri dan mendapatkan nilai sudutnya. Sekarang awal interval sudut lebih kecil dari akhir, dan kita dapat menulis interval penyelesaian tanpa memperhitungkan periode:
Mengingat bahwa interval tersebut akan diulang berkali-kali setelah sejumlah rotasi bilangan bulat, kita memperoleh solusi umum dengan mempertimbangkan periode sinus:
Kita memberi tanda kurung karena pertidaksamaannya sangat ketat, dan kita memilih titik-titik pada lingkaran yang sesuai dengan ujung-ujung interval.
Bandingkan jawaban yang Anda terima dengan rumus solusi umum yang kami berikan pada kuliah.
Menjawab. 
.
Metode ini bagus untuk memahami dari mana rumus solusi umum pertidaksamaan trigon paling sederhana berasal. Selain itu, berguna bagi mereka yang terlalu malas untuk mempelajari semua rumus yang rumit tersebut. Namun, metodenya sendiri juga tidak mudah; pilihlah pendekatan solusi mana yang paling nyaman bagi Anda.
Untuk menyelesaikan pertidaksamaan trigonometri, Anda juga dapat menggunakan grafik fungsi yang memiliki garis bantu, mirip dengan metode yang ditunjukkan menggunakan lingkaran satuan. Jika Anda tertarik, cobalah mencari tahu sendiri pendekatan solusi ini. Berikut ini kita akan menggunakan rumus umum untuk menyelesaikan pertidaksamaan trigonometri sederhana.
Soal No.10. Selesaikan ketimpangan.
Mari kita gunakan rumus untuk penyelesaian umum, dengan mempertimbangkan fakta bahwa pertidaksamaan tidak tegas:
Dalam kasus kami, kami mendapatkan:
Menjawab. 
Soal No.11. Selesaikan ketimpangan.
Mari kita gunakan rumus solusi umum untuk pertidaksamaan ketat yang bersesuaian:
Menjawab. 
.
Soal No.12. Selesaikan pertidaksamaan: a) ; B) .
Dalam pertidaksamaan tersebut, tidak perlu terburu-buru menggunakan rumus penyelesaian umum atau lingkaran trigonometri; cukup mengingat rentang nilai sinus dan kosinus.
a) Sejak 
, maka ketimpangan tersebut tidak masuk akal. Oleh karena itu, tidak ada solusi.
b) Karena sama halnya, sinus dari argumen apa pun selalu memenuhi pertidaksamaan yang ditentukan dalam kondisi. Oleh karena itu, semua nilai riil argumen tersebut memenuhi pertidaksamaan.
Menjawab. a) tidak ada solusi; B) .
Masalah 13. Selesaikan ketimpangan 
.
