Akhirnya, saya mendapatkan topik yang luas dan telah lama ditunggu-tunggu ini. geometri analitik . Pertama, sedikit tentang bagian ini matematika yang lebih tinggi…. Pasti Anda sekarang ingat kursus geometri sekolah dengan berbagai teorema, pembuktiannya, gambarnya, dll. Apa yang disembunyikan, mata pelajaran yang tidak disukai dan sering kali tidak jelas bagi sebagian besar siswa. Anehnya, geometri analitik mungkin tampak lebih menarik dan mudah diakses. Apa arti dari kata sifat “analitis”? Dua frasa matematika klise segera terlintas dalam pikiran: “metode solusi grafis” dan “ metode analitis solusi". Metode grafis , tentu saja, dikaitkan dengan konstruksi grafik dan gambar. Analitis sama metode melibatkan pemecahan masalah terutama melalui operasi aljabar. Dalam hal ini, algoritma untuk menyelesaikan hampir semua masalah geometri analitik sederhana dan transparan, seringkali cukup untuk diterapkan dengan hati-hati formula yang diperlukan- dan jawabannya sudah siap! Tidak, tentu saja, itu tidak akan mungkin terjadi tanpa gambar sama sekali, dan terlebih lagi, untuk pemahaman yang lebih baik Saya akan mencoba memberikan lebih banyak materi daripada yang diperlukan.
Kursus pelajaran geometri yang baru dibuka tidak berpura-pura lengkap secara teoritis; tetapi difokuskan pada pemecahan masalah-masalah praktis. Saya hanya akan memasukkan dalam kuliah saya apa yang, dari sudut pandang saya, penting secara praktis. Jika Anda membutuhkan lebih banyak informasi lengkap Untuk subbagian apa pun, saya merekomendasikan literatur yang cukup mudah diakses berikut ini:
1) Suatu hal yang sudah dikenal oleh beberapa generasi: Buku teks sekolah tentang geometri, penulis - L.S. Atanasyan dan Perusahaan. Gantungan ruang ganti sekolah ini sudah melalui 20 (!) cetak ulang, yang tentu saja bukan batasnya.
2) Geometri dalam 2 volume. Penulis L.S. Atanasyan, Bazylev V.T.. Ini adalah literatur untuk sekolah menengah atas, Anda akan perlu jilid pertama. Tugas yang jarang ditemui mungkin luput dari perhatian saya, dan tutorial akan memberikan bantuan yang sangat berharga.
Kedua buku tersebut dapat diunduh secara online gratis. Selain itu, Anda dapat menggunakan arsip saya dengan solusi siap pakai, yang dapat ditemukan di halaman Unduh contoh dalam matematika tingkat tinggi.
Di antara alat-alat tersebut, saya kembali mengusulkan pengembangan saya sendiri - paket perangkat lunak dalam geometri analitik, yang akan sangat menyederhanakan hidup dan menghemat banyak waktu.
Diasumsikan bahwa pembaca sudah familiar dengan dasarnya konsep geometris dan gambar: titik, garis, bidang, segitiga, jajar genjang, jajar genjang, kubus, dll. Dianjurkan untuk mengingat beberapa teorema, setidaknya teorema Pythagoras, halo repeater)
Dan sekarang kita akan membahas secara berurutan: konsep vektor, tindakan dengan vektor, koordinat vektor. Saya sarankan membaca lebih lanjut artikel yang paling penting Produk titik dari vektor, dan juga Vektor dan hasil kali campuran vektor. Tugas lokal - Pembagian segmen dalam hal ini - juga tidak akan berlebihan. Berdasarkan informasi di atas, Anda dapat menguasainya persamaan garis pada bidang Dengan contoh solusi yang paling sederhana, yang akan memungkinkan belajar memecahkan masalah geometri. Artikel berikut juga bermanfaat: Persamaan pesawat di luar angkasa, Persamaan garis dalam ruang, Masalah dasar pada garis lurus dan bidang, bagian geometri analitik lainnya. Tentu saja, tugas-tugas standar akan dipertimbangkan sepanjang proses.
Konsep vektor. vektor gratis
Pertama, mari kita ulangi definisi sekolah tentang vektor. Vektor ditelepon diarahkan segmen yang awal dan akhirnya ditunjukkan:
DI DALAM pada kasus ini awal ruas adalah titik, ujung ruas adalah titik. Vektor itu sendiri dilambangkan dengan . Arah sangat penting, jika Anda memindahkan panah ke ujung lain segmen, Anda mendapatkan vektor, dan ini sudah menjadi vektor yang sama sekali berbeda. Konsep vektor mudah diidentikkan dengan gerak tubuh fisik: Setuju, memasuki pintu institut atau meninggalkan pintu institut adalah hal yang sangat berbeda.
Lebih mudah untuk mempertimbangkan titik-titik individual pada suatu bidang atau ruang sebagai apa yang disebut vektor nol. Untuk vektor seperti itu, akhir dan permulaannya bertepatan.
!!! Catatan: Di sini dan selanjutnya, kita dapat berasumsi bahwa vektor-vektor terletak pada bidang yang sama atau kita dapat berasumsi bahwa vektor-vektor tersebut terletak di ruang - intisari materi yang disajikan berlaku baik untuk bidang maupun ruang.
Sebutan: Banyak yang langsung memperhatikan tongkat tanpa panah di peruntukannya dan berkata, ada juga panah di atasnya! Benar, Anda dapat menuliskannya dengan tanda panah: , tetapi bisa juga entri yang akan saya gunakan di masa depan. Mengapa? Rupanya, kebiasaan ini berkembang karena alasan praktis; penembak saya di sekolah dan universitas ternyata berukuran terlalu berbeda dan berbulu lebat. DI DALAM literatur pendidikan terkadang mereka tidak mempermasalahkan tulisan paku sama sekali, melainkan menyorot huruf-hurufnya dalam huruf tebal: , menyiratkan bahwa itu adalah vektor.
Itu tadi stilistika, dan sekarang tentang cara menulis vektor:
1) Vektor dapat ditulis dengan dua huruf latin kapital: 
dan seterusnya. Dalam hal ini, huruf pertama Perlu menunjukkan titik awal vektor, dan huruf kedua menunjukkan titik akhir vektor.
2) Vektor juga ditulis dengan huruf latin kecil:
Khususnya, agar singkatnya vektor kita dapat didesain ulang menjadi kecil huruf latin.
Panjang atau modul Bukan vektor nol disebut panjang segmen. Panjang vektor nol adalah nol. Logis.
Panjang vektor ditunjukkan dengan tanda modulus: ,
Kita akan mempelajari cara mencari panjang sebuah vektor (atau kita akan mengulanginya, tergantung siapa) nanti.
Demikianlah informasi dasar tentang vektor yang familiar bagi semua anak sekolah. Dalam geometri analitik, yang disebut vektor gratis.
Untuk membuatnya lebih sederhana - vektor dapat diplot dari titik mana pun:
Kita terbiasa menyebut vektor-vektor tersebut sama (definisi vektor-vektor yang sama akan diberikan di bawah), tetapi murni dari titik matematika tampilannya adalah VEKTOR YANG SAMA atau vektor gratis. Mengapa gratis? Karena dalam menyelesaikan masalah, Anda dapat “melampirkan” vektor ini atau itu ke titik APAPUN pada bidang atau ruang yang Anda perlukan. Ini adalah fitur yang sangat keren! Bayangkan sebuah vektor dengan panjang dan arah yang berubah-ubah - vektor tersebut dapat “dikloning” jumlah yang tak terbatas waktu dan di titik mana pun dalam ruang, faktanya, ia ada DI MANA SAJA. Ada pepatah mahasiswa: Setiap dosen peduli dengan vektor. Lagi pula, ini bukan hanya sajak yang jenaka, semuanya benar secara matematis - vektor juga dapat dilampirkan di sana. Tapi jangan buru-buru bergembira, yang sering menderita adalah siswanya sendiri =)
Jadi, vektor gratis- Ini sekelompok segmen berarah identik. Definisi sekolah vektor yang diberikan di awal paragraf: “Segmen berarah disebut vektor…” menyiratkan spesifik segmen berarah yang diambil dari himpunan tertentu, yang dilampirkan titik tertentu pesawat atau luar angkasa.
Perlu dicatat bahwa dari sudut pandang fisika, konsep vektor bebas umumnya salah, dan sudut penerapan vektor itu penting. Memang benar, pukulan langsung kekuatan yang setara di hidung atau di dahi, berhentilah mengembangkan contoh bodoh saya, ini akan menimbulkan konsekuensi yang berbeda. Namun, tidak bebas vektor juga ditemukan di vyshmat (jangan kesana :)).
Tindakan dengan vektor. Kolinearitas vektor
Kursus geometri sekolah mencakup sejumlah tindakan dan aturan dengan vektor: penjumlahan menurut aturan segitiga, penjumlahan menurut aturan jajar genjang, aturan selisih vektor, perkalian vektor dengan bilangan, hasil kali skalar vektor, dan sebagainya. Sebagai titik awal, mari kita ulangi dua aturan yang sangat relevan untuk memecahkan masalah geometri analitik.
Aturan penjumlahan vektor menggunakan aturan segitiga
Pertimbangkan dua vektor sembarang bukan nol dan : 
Anda perlu mencari jumlah vektor-vektor ini. Karena semua vektor dianggap bebas, maka kita akan menyisihkan vektor tersebut dari akhir vektor: 
Jumlah vektor adalah vektor. Untuk pemahaman yang lebih baik tentang aturan tersebut, disarankan untuk menyertakannya arti fisik: biarkan suatu benda bergerak sepanjang suatu vektor, dan kemudian sepanjang suatu vektor. Maka jumlah vektor-vektor tersebut adalah vektor lintasan yang dihasilkan dengan titik awal di titik berangkat dan berakhir di titik tiba. Aturan serupa dirumuskan untuk jumlah sejumlah vektor. Seperti yang mereka katakan, tubuh dapat bergerak dengan sangat miring secara zigzag, atau mungkin dengan autopilot - sepanjang vektor penjumlahan yang dihasilkan.
Omong-omong, jika vektornya ditunda dari dimulai vektor, maka kita mendapatkan persamaannya aturan jajaran genjang penambahan vektor.
Pertama, tentang kolinearitas vektor. Kedua vektor tersebut disebut segaris, jika keduanya terletak pada satu garis atau sejajar. Secara kasar, kita berbicara tentang vektor paralel. Namun dalam kaitannya dengan mereka, kata sifat “collinear” selalu digunakan.
Bayangkan dua vektor segaris. Jika anak panah dari vektor-vektor tersebut diarahkan pada arah yang sama, maka vektor-vektor tersebut disebut diarahkan bersama. Jika panah mengarah ke sisi yang berbeda, maka vektornya adalah arah berlawanan.
Sebutan: kolinearitas vektor ditulis dengan simbol paralelisme biasa: , sedangkan perincian dapat dilakukan: (vektor-vektor searah) atau (vektor-vektor berlawanan arah).
Pekerjaan vektor bukan nol suatu bilangan adalah suatu vektor yang panjangnya sama dengan , dan vektor-vektor tersebut berarah dan berlawanan arah pada .
Aturan mengalikan vektor dengan bilangan lebih mudah dipahami dengan bantuan gambar: 
Mari kita lihat lebih detail:
1 arah. Jika pengalinya negatif, maka vektornya mengubah arah sebaliknya.
2) Panjang. Jika pengali terdapat di dalam atau , maka panjang vektornya berkurang. Jadi, panjang vektor adalah setengah panjang vektor. Jika pengganda modulo lebih dari satu, maka panjang vektor meningkat pada waktunya.
3) Harap dicatat bahwa semua vektor adalah segaris, sedangkan satu vektor dinyatakan melalui vektor lainnya, misalnya . Hal sebaliknya juga benar: jika suatu vektor dapat dinyatakan melalui vektor lain, maka vektor-vektor tersebut harus kolinear. Dengan demikian: jika kita mengalikan vektor dengan angka, kita mendapatkan kolinear(relatif terhadap aslinya) vektor.
4) Vektor-vektornya mempunyai arah yang sama. Vektor dan juga diarahkan bersama. Setiap vektor pada golongan pertama mempunyai arah yang berlawanan terhadap vektor mana pun pada golongan kedua.
Vektor manakah yang sama?
Dua buah vektor dikatakan sama jika arahnya sama dan panjangnya sama. Perhatikan bahwa ko-arah menyiratkan kolinearitas vektor. Definisi tersebut akan menjadi tidak akurat (berlebihan) jika kita mengatakan: “Dua vektor adalah sama jika keduanya segaris, searah, dan mempunyai panjang yang sama.”
Dari sudut pandang konsep vektor bebas, vektor yang sama– ini adalah vektor yang sama, yang telah dibahas pada paragraf sebelumnya.
Koordinat vektor pada bidang dan ruang
Poin pertama adalah memperhatikan vektor pada bidang. Mari kita gambarkan sistem koordinat persegi panjang Cartesian dan plot dari titik asal lajang vektor dan :
Vektor dan ortogonal. Ortogonal = Tegak Lurus. Saya menganjurkan agar Anda perlahan-lahan membiasakan diri dengan istilah-istilah tersebut: alih-alih paralelisme dan tegak lurus, kami menggunakan kata-kata tersebut masing-masing kolinearitas Dan ortogonalitas.
Penamaan: Ortogonalitas vektor ditulis dengan simbol tegak lurus biasa, contoh: .
Vektor yang ditinjau disebut koordinat vektor atau ort. Vektor-vektor ini terbentuk dasar di permukaan. Menurut saya, apa yang mendasarinya sudah jelas secara intuitif bagi banyak orang Informasi rinci dapat ditemukan di artikel Ketergantungan vektor yang linier (bukan). Dasar vektor Dengan kata sederhana, basis dan asal koordinat menentukan keseluruhan sistem - ini adalah semacam fondasi di mana kehidupan geometris yang penuh dan kaya bermuara.
Terkadang dasar yang dibangun disebut ortonormal dasar bidang: "orto" - karena vektor koordinatnya ortogonal, kata sifat "dinormalisasi" berarti satuan, mis. panjang vektor basis sama dengan satu.
Penamaan: dasarnya biasanya ditulis dalam tanda kurung, di dalamnya dalam urutan yang ketat vektor basis dicantumkan, misalnya: . Mengkoordinasikan vektor itu dilarang mengatur kembali.
Setiap vektor bidang satu-satunya jalan diekspresikan sebagai: 
, Di mana - angka yang disebut koordinat vektor dalam dasar ini. Dan ekspresi itu sendiri 
ditelepon dekomposisi vektorberdasarkan dasar .
Makan malam disajikan:
Mari kita mulai dengan huruf pertama alfabet: . Gambar tersebut dengan jelas menunjukkan bahwa ketika menguraikan vektor menjadi basis, vektor yang baru saja dibahas digunakan:
1) aturan mengalikan vektor dengan bilangan: dan ;
2) penjumlahan vektor menurut aturan segitiga: .
Sekarang secara mental gambarkan vektor dari titik lain mana pun di bidang. Jelas sekali bahwa pembusukannya akan “mengikutinya tanpa henti”. Ini dia, kebebasan vektor - vektor “membawa segala sesuatu dengan dirinya sendiri.” Sifat ini tentu saja berlaku untuk vektor apa pun. Lucunya, vektor basis (bebas) itu sendiri tidak harus diplot dari titik asal; satu dapat digambar, misalnya, di kiri bawah, dan yang lainnya di kanan atas, dan tidak ada yang berubah! Benar, Anda tidak perlu melakukan ini, karena guru juga akan menunjukkan orisinalitas dan memberi Anda “penghargaan” di tempat yang tidak terduga.
Vektor menggambarkan dengan tepat aturan perkalian suatu vektor dengan suatu bilangan, vektor searah dengan vektor alas, vektor arahnya berlawanan dengan vektor alas. Untuk vektor-vektor ini, salah satu koordinatnya sama dengan nol; Anda dapat menuliskannya dengan cermat seperti ini:
Dan vektor basisnya adalah seperti ini: (sebenarnya, vektor tersebut diekspresikan melalui dirinya sendiri).
Dan akhirnya: , . Ngomong-ngomong, apa itu pengurangan vektor, dan kenapa saya tidak membahas aturan pengurangannya? Di suatu tempat di aljabar linier, saya tidak ingat di mana, saya catat itu pengurangan kasus spesial tambahan. Jadi, pemuaian vektor “de” dan “e” dengan mudah ditulis sebagai penjumlahan: , 
. Susun ulang suku-sukunya dan lihat pada gambar seberapa baik penjumlahan vektor-vektor lama menurut aturan segitiga bekerja dalam situasi ini.
Dekomposisi bentuk yang dipertimbangkan 
kadang-kadang disebut dekomposisi vektor dalam sistem ort(yaitu dalam sistem vektor satuan). Namun ini bukan satu-satunya cara untuk menulis vektor; opsi berikut ini umum digunakan:
Atau dengan tanda sama dengan:
Vektor basisnya sendiri ditulis sebagai berikut: dan
Artinya, koordinat vektor ditunjukkan dalam tanda kurung. DI DALAM masalah praktis Ketiga opsi perekaman digunakan.
Saya ragu apakah saya harus berbicara atau tidak, tetapi saya akan tetap mengatakannya: koordinat vektor tidak dapat diatur ulang. Tepatnya di tempat pertama kita tuliskan koordinat yang sesuai dengan vektor satuan, ketat di tempat kedua kita tuliskan koordinat yang sesuai dengan vektor satuan. Memang, dan merupakan dua vektor yang berbeda.
Kami menemukan koordinat di pesawat. Sekarang mari kita lihat vektor dalam ruang tiga dimensi, hampir semuanya sama di sini! Itu hanya akan menambah satu koordinat lagi. Sulit untuk membuat gambar tiga dimensi, jadi saya akan membatasi diri pada satu vektor, yang untuk kesederhanaan saya akan kesampingkan dari titik asal: 
Setiap vektor ruang tiga dimensi Bisa satu-satunya jalan berkembang secara ortonormal: 
, dimana koordinat vektor (bilangan) pada basis ini.
Contoh dari gambar: 
. Mari kita lihat cara kerja aturan vektor di sini. Pertama, kalikan vektor dengan angka: (panah merah), (panah hijau), dan (panah raspberry). Kedua, berikut adalah contoh penjumlahan beberapa, dalam hal ini tiga, vektor: . Penjumlahan vektor dimulai pada titik awal berangkat (awal vektor) dan berakhir pada titik akhir kedatangan (akhir vektor).
Semua vektor ruang tiga dimensi, tentu saja, juga bebas; cobalah untuk secara mental mengesampingkan vektor tersebut dari titik lain mana pun, dan Anda akan memahami bahwa penguraiannya “akan tetap bersamanya”.
Mirip dengan case datar, selain tulisan 
versi dengan tanda kurung banyak digunakan: baik .
Jika satu (atau dua) vektor koordinat hilang dalam pemuaian, maka nol ditempatkan pada tempatnya. Contoh:
vektor (dengan cermat 
) - Mari menulis ;
vektor (dengan cermat 
) - Mari menulis ;
vektor (dengan cermat 
) - Mari menulis .
Vektor basis ditulis sebagai berikut:
Ini, mungkin, adalah pengetahuan teoretis minimum yang diperlukan untuk memecahkan masalah geometri analitik. Mungkin ada banyak istilah dan definisi, jadi saya sarankan agar orang bodoh membaca dan memahaminya kembali informasi ini lagi. Dan akan bermanfaat bagi setiap pembaca untuk merujuk pada pelajaran dasar dari waktu ke waktu agar dapat mengasimilasi materi dengan lebih baik. Kolinearitas, ortogonalitas, basis ortonormal, dekomposisi vektor - konsep ini dan konsep lainnya akan sering digunakan di masa depan. Saya ingin mencatat bahwa materi situs tidak cukup untuk lulus ujian teoretis atau kolokium geometri, karena saya dengan hati-hati mengenkripsi semua teorema (dan tanpa bukti) - sehingga merugikan gaya ilmiah presentasi, tetapi merupakan nilai tambah untuk pemahaman Anda tentang subjek. Untuk menerima informasi teoretis terperinci, silakan tunduk pada Profesor Atanasyan.
Dan kita beralih ke bagian praktis:
Masalah paling sederhana dari geometri analitik.
Tindakan dengan vektor dalam koordinat
Sangat disarankan untuk mempelajari cara menyelesaikan tugas yang akan dibahas sepenuhnya secara otomatis, dan rumusnya menghafal, bahkan tidak mengingatnya secara spesifik, mereka akan mengingatnya sendiri =) Ini sangat penting, karena soal geometri analitik lainnya didasarkan pada contoh dasar yang paling sederhana, dan sayang untuk disia-siakan Waktu tambahan untuk memakan pion. Tidak perlu mengencangkan kancing atas baju Anda; banyak hal yang Anda kenal dari sekolah.
Penyajian materi akan mengikuti alur paralel, baik untuk bidang datar maupun ruang. Karena semua rumusnya... Anda akan melihatnya sendiri.
Bagaimana cara mencari vektor dari dua titik?
Jika dua titik pada bidang dan diberikan, maka vektor tersebut mempunyai koordinat sebagai berikut: 
Jika dua titik dalam ruang dan diberikan, maka vektor tersebut mempunyai koordinat sebagai berikut:
Itu adalah, dari koordinat ujung vektor Anda perlu mengurangi koordinat yang sesuai awal vektor.
Latihan: Untuk titik yang sama, tuliskan rumus mencari koordinat vektor. Rumus di akhir pelajaran.
Contoh 1
Diberikan dua titik pada bidang dan . Temukan koordinat vektor
Larutan: sesuai dengan rumus yang sesuai:
Sebagai alternatif, entri berikut dapat digunakan:
Aesthetes akan memutuskan ini:
Secara pribadi, saya sudah terbiasa dengan rekaman versi pertama.
Menjawab:
Sesuai dengan kondisi, tidak perlu membuat gambar (yang khas untuk masalah geometri analitik), tetapi untuk memperjelas beberapa poin untuk boneka, saya tidak akan malas: 
Anda pasti perlu memahaminya perbedaan antara koordinat titik dan koordinat vektor:
Koordinat titik adalah koordinat biasa di sistem persegi panjang koordinat Pasang poin bidang koordinat Saya pikir semua orang bisa melakukannya dari kelas 5-6. Setiap titik memiliki tempat yang ketat di bidangnya, dan tidak dapat dipindahkan ke mana pun.
Koordinat vektor– ini adalah perluasannya menurut dasar, dalam hal ini. Vektor apa pun bebas, jadi jika perlu, kita dapat dengan mudah memindahkannya dari titik lain pada bidang tersebut. Menariknya, untuk vektor Anda tidak perlu membuat sumbu atau sistem koordinat persegi panjang sama sekali; Anda hanya memerlukan basis, dalam hal ini basis ortonormal dari bidang tersebut.
Pencatatan koordinat titik dan koordinat vektor nampaknya serupa: , dan arti koordinat sangat berbeda, dan Anda harus menyadari perbedaan ini. Perbedaan ini tentu saja juga berlaku pada ruang.
Hadirin sekalian, mari kita isi tangan kita:
Contoh 2
a) Poin dan diberikan. Temukan vektor dan .
b) Poin diberikan 
Dan . Temukan vektor dan .
c) Poin dan diberikan. Temukan vektor dan .
d) Poin diberikan. Temukan vektor 
.
Mungkin itu cukup. Ini adalah contoh untuk keputusan independen, cobalah untuk tidak mengabaikannya, itu akan membuahkan hasil ;-). Tidak perlu membuat gambar. Solusi dan jawaban di akhir pelajaran.
Apa yang penting ketika menyelesaikan masalah geometri analitik? Sangatlah penting untuk berhati-hati agar tidak membuat kesalahan “dua tambah dua sama dengan nol”. Saya segera meminta maaf jika saya melakukan kesalahan di suatu tempat =)
Bagaimana cara mencari panjang suatu ruas?
Panjangnya, sebagaimana telah disebutkan, ditunjukkan dengan tanda modulus.
Jika diberikan dua titik pada bidang dan , maka panjang ruas tersebut dapat dihitung dengan menggunakan rumus
Jika ada dua titik dalam ruang dan diberikan, maka panjang ruas tersebut dapat dihitung dengan menggunakan rumus
Catatan: Rumusnya akan tetap benar jika koordinat yang bersangkutan ditukar: dan , tetapi opsi pertama lebih standar
Contoh 3
Larutan: sesuai dengan rumus yang sesuai:
Menjawab: 
Untuk lebih jelasnya, saya akan membuat gambar 
Segmen garis - ini bukan vektor, dan, tentu saja, Anda tidak dapat memindahkannya ke mana pun. Selain itu, jika Anda menggambar menurut skala: 1 satuan. = 1 cm (dua sel buku catatan), maka jawaban yang dihasilkan dapat diperiksa dengan penggaris biasa dengan cara mengukur langsung panjang ruas tersebut.
Ya, solusinya singkat, tetapi masih ada beberapa solusi lagi poin penting yang ingin saya jelaskan:
Pertama, dalam jawaban kami mencantumkan dimensi: “satuan”. Kondisinya tidak menyebutkan APA itu, milimeter, sentimeter, meter atau kilometer. Oleh karena itu, solusi yang benar secara matematis adalah rumusan umum: "unit" - disingkat "unit".
Kedua, mari kita ulangi materi sekolah, yang berguna tidak hanya untuk masalah yang dipertimbangkan:
perhatikan teknik penting – menghapus pengganda dari bawah root. Sebagai hasil perhitungan, kami mendapatkan hasil dan gaya matematika yang baik melibatkan penghapusan faktor dari bawah akar (jika memungkinkan). Secara lebih rinci prosesnya terlihat seperti ini: 
. Tentu saja, membiarkan jawaban apa adanya bukanlah suatu kesalahan - tetapi tentu saja akan menjadi kelemahan dan argumen yang kuat untuk membuat guru berdalih.
Berikut kasus umum lainnya: 
Seringkali jumlahnya cukup di akarnya jumlah yang besar, Misalnya . Apa yang harus dilakukan dalam kasus seperti itu? Dengan menggunakan kalkulator, kita periksa apakah bilangan tersebut habis dibagi 4: . Ya, itu benar-benar terbagi, jadi: 
. Atau mungkin angkanya bisa dibagi 4 lagi? . Dengan demikian: 
. Di nomor tersebut angka terakhir aneh, jadi membaginya dengan 4 untuk ketiga kalinya jelas tidak akan berhasil. Mari kita coba bagi dengan sembilan: . Sebagai akibat:
Siap.
Kesimpulan: jika di bawah akar kita mendapatkan bilangan yang tidak dapat diekstraksi secara keseluruhan, maka kita coba menghilangkan faktor tersebut dari bawah akar - dengan menggunakan kalkulator kita memeriksa apakah bilangan tersebut habis dibagi: 4, 9, 16, 25, 36, 49, dll.
Selama pengambilan keputusan berbagai tugas akar permasalahan adalah hal yang umum, selalu berusaha untuk mengekstrak faktor-faktor dari bawah akar untuk menghindari nilai yang lebih rendah dan masalah yang tidak perlu dalam menyelesaikan solusi Anda berdasarkan komentar guru.
Mari kita ulangi juga akar kuadrat dan pangkat lainnya: 
Aturan untuk tindakan dengan derajat masuk pandangan umum bisa ditemukan di buku pelajaran sekolah tentang aljabar, tapi menurut saya dari contoh yang diberikan sudah jelas semuanya atau hampir semuanya.
Tugas untuk solusi mandiri dengan segmen dalam ruang:
Contoh 4
Poin dan diberikan. Temukan panjang segmen tersebut.
Solusi dan jawabannya ada di akhir pelajaran.
Bagaimana cara mencari panjang suatu vektor?
Jika vektor bidang diberikan, maka panjangnya dihitung dengan rumus.
Jika diberikan vektor ruang, maka panjangnya dihitung dengan rumus 
.
Pada artikel ini kita akan membahas secara rinci konsep perkalian silang dua vektor. Kami akan memberi definisi yang diperlukan, kita akan menulis rumus untuk mencari koordinat suatu produk vektor, mencantumkan dan membenarkan sifat-sifatnya. Setelah ini, kita akan membahas arti geometris dari produk vektor dua vektor dan mempertimbangkan solusi untuk berbagai contoh tipikal.
Navigasi halaman.
Definisi perkalian silang.
Sebelum mendefinisikan perkalian vektor, mari kita pahami orientasi rangkap tiga vektor dalam ruang tiga dimensi.
Mari kita gambarkan vektor dari satu titik. Tergantung arah vektornya, ketiganya bisa kanan atau kiri. Mari kita lihat dari ujung vektor bagaimana belokan terpendek dari vektor ke . Jika putaran terpendek terjadi berlawanan arah jarum jam, maka rangkap tiga vektornya disebut Kanan, jika tidak - kiri.
Sekarang mari kita ambil dua vektor yang tidak segaris dan . Mari kita plot vektor dan dari titik A. Mari kita buat beberapa vektor yang tegak lurus terhadap keduanya dan dan . Jelasnya, ketika membangun sebuah vektor, kita dapat melakukan dua hal, memberikannya satu arah atau sebaliknya (lihat ilustrasi).
Bergantung pada arah vektornya, triplet vektor yang terurut dapat bertangan kanan atau bertangan kiri.
Hal ini membawa kita lebih dekat pada definisi perkalian vektor. Ini diberikan untuk dua vektor yang didefinisikan dalam sistem koordinat persegi panjang dalam ruang tiga dimensi.
Definisi.
Perkalian silang dua buah vektor dan , ditentukan dalam sistem koordinat persegi panjang ruang tiga dimensi, disebut vektor sedemikian rupa sehingga
Produk silang vektor dan dilambangkan sebagai .
Koordinat hasil kali vektor.
Sekarang kita akan memberikan definisi kedua dari perkalian vektor, yang memungkinkan Anda mencari koordinatnya dari koordinat vektor yang diberikan dan.
Definisi.
Dalam sistem koordinat persegi panjang ruang tiga dimensi produk vektor dua vektor 
Dan 
adalah vektor, dimana adalah vektor koordinatnya.
Definisi ini memberi kita perkalian silang dalam bentuk koordinat.
Lebih mudah untuk merepresentasikan perkalian silang sebagai determinan matriks persegi orde ketiga, baris pertama berisi vektor satuan, baris kedua berisi koordinat vektor, dan baris ketiga berisi koordinat vektor pada sistem koordinat persegi panjang yang diberikan: 
Jika kita memperluas determinan ini ke dalam elemen-elemen baris pertama, kita memperoleh persamaan dari definisi produk vektor dalam koordinat (jika perlu, lihat artikel): 
Perlu dicatat bahwa bentuk koordinat perkalian vektor sepenuhnya sesuai dengan definisi yang diberikan pada paragraf pertama artikel ini. Selain itu, kedua definisi perkalian silang ini setara. Bukti fakta ini dapat Anda lihat pada buku yang tercantum di akhir artikel.
Sifat-sifat produk vektor.
Karena hasil kali vektor dalam koordinat dapat direpresentasikan sebagai determinan matriks, hal berikut dapat dengan mudah dibenarkan berdasarkan: sifat produk silang:
Sebagai contoh, mari kita buktikan sifat antikomutatif suatu produk vektor.
A-priori 
Dan 
. Kita mengetahui bahwa nilai determinan suatu matriks akan dibalik jika dua barisnya ditukar, oleh karena itu, 
, yang membuktikan sifat antikomutatif suatu produk vektor.
Produk vektor - contoh dan solusi.
Pada dasarnya ada tiga jenis masalah.
Dalam soal tipe pertama, panjang dua vektor dan sudut di antara keduanya diberikan, dan Anda perlu mencari panjang hasil kali vektor. Dalam hal ini rumus yang digunakan 
.
Contoh.
Tentukan panjang hasil kali vektor dari vektor-vektor dan , jika diketahui 
.
Larutan.
Kita mengetahui dari definisi bahwa panjang hasil kali vektor vektor dan sama dengan hasil kali panjang vektor dan sinus sudut di antara keduanya, oleh karena itu, 
.
Menjawab:
.
Soal tipe kedua berkaitan dengan koordinat vektor, di mana hasil kali vektor, panjangnya atau apa pun dicari melalui koordinat vektor yang diberikan. Dan .
Ada banyak potensi di sini berbagai pilihan. Misalnya, bukan koordinat vektor dan yang dapat ditentukan, tetapi pemuaiannya koordinat vektor baik 
dan , atau vektor dan dapat ditentukan dengan koordinat titik awal dan titik akhir.
Mari kita lihat contoh-contoh tipikal.
Contoh.
Dua vektor diberikan dalam sistem koordinat persegi panjang 
. Temukan produk silangnya.
Larutan.
Menurut definisi kedua, hasil kali vektor dua vektor dalam koordinat ditulis sebagai: 
Kita akan mendapatkan hasil yang sama jika hasil perkalian vektor ditulis dalam bentuk determinan 
Menjawab:
.
Contoh.
Temukan panjang produk vektor dari vektor dan , di mana adalah vektor satuan dari sistem koordinat kartesius persegi panjang.
Larutan.
Pertama kita cari koordinat hasil kali vektornya 
dalam sistem koordinat persegi panjang tertentu.
Karena vektor dan memiliki koordinat dan masing-masing (jika perlu, lihat artikel koordinat vektor dalam sistem koordinat persegi panjang), maka dengan definisi kedua dari produk vektor kita memiliki 
Artinya, produk vektor memiliki koordinat dalam sistem koordinat tertentu.
Kita mencari panjang suatu hasil kali vektor sebagai akar kuadrat dari jumlah kuadrat koordinatnya (kita memperoleh rumus panjang suatu vektor pada bagian mencari panjang suatu vektor):
Menjawab:
.
Contoh.
Dalam bentuk persegi panjang sistem kartesius koordinat koordinat tiga titik diberikan. Temukan beberapa vektor yang tegak lurus dan pada waktu yang sama.
Larutan.
Vektor dan mempunyai koordinat dan masing-masing (lihat artikel mencari koordinat suatu vektor melalui koordinat titik). Jika kita mencari hasil perkalian vektor dari vektor-vektor dan , maka menurut definisi vektor tersebut adalah vektor yang tegak lurus terhadap dan terhadap , yaitu solusi untuk masalah kita. Mari kita temukan dia 
Menjawab:
- salah satu vektor tegak lurus.
Dalam soal tipe ketiga, keterampilan menggunakan sifat-sifat perkalian vektor vektor diuji. Setelah menerapkan properti, rumus yang sesuai diterapkan.
Contoh.
Vektor-vektornya tegak lurus dan panjangnya masing-masing 3 dan 4. Temukan panjang hasil perkalian silang 
.
Larutan.
Berdasarkan sifat distributif suatu perkalian vektor, kita dapat menulis 
Karena sifat kombinasionalnya, kita menghilangkan koefisien numerik dari tanda perkalian vektor pada ekspresi terakhir: 
Hasil kali vektor dan sama dengan nol, karena 
Dan 
, Kemudian .
Karena hasil kali vektor bersifat antikomutatif, maka .
Jadi, dengan menggunakan sifat-sifat perkalian vektor, kita sampai pada persamaan 
.
Dengan syarat, vektor-vektor dan tegak lurus, yaitu sudut antara keduanya sama dengan . Artinya, kita memiliki semua data untuk mencari panjang yang dibutuhkan 
Menjawab:
.
Arti geometris dari produk vektor.
Menurut definisi, panjang produk vektor dari vektor adalah 
. Dan dari mata kuliah geometri sekolah menengah atas Kita tahu bahwa luas segitiga sama dengan setengah hasil kali panjang kedua sisi segitiga dan sinus sudut di antara keduanya. Oleh karena itu, panjang hasil kali vektor sama dengan dua kali luas segitiga yang sisi-sisinya merupakan vektor dan , jika diplot dari satu titik. Dengan kata lain, panjang hasil kali vektor vektor-vektor dan sama dengan luas jajar genjang yang sisi-sisinya dan dan sudut antara keduanya sama dengan . Ini makna geometris produk vektor.
Definisi. Hasil kali vektor dari vektor a (perkalian) dan vektor non-kolinier (perkalian) adalah vektor ketiga c (perkalian), yang dibangun sebagai berikut:
1) modulusnya numerik sama dengan luas jajaran genjang pada Gambar. 155), dibangun di atas vektor, yaitu sama dengan arah tegak lurus bidang jajar genjang tersebut;
3) dalam hal ini, arah vektor c dipilih (dari dua kemungkinan) sehingga vektor c membentuk sistem tangan kanan (§ 110).
Sebutan: atau
Selain definisi. Jika vektor-vektornya kolinear, maka mengingat gambar tersebut (dengan syarat) merupakan jajar genjang, maka wajar jika luasnya nol. Oleh karena itu, hasil kali vektor dari vektor-vektor yang segaris dianggap sama dengan vektor nol.
Karena vektor nol dapat diberikan ke arah mana pun, perjanjian ini tidak bertentangan dengan paragraf 2 dan 3 definisi.
Catatan 1. Dalam istilah “perkalian silang” kata pertama menunjukkan bahwa hasil suatu tindakan adalah vektor (bukan produk skalar; Menikahi § 104, komentar 1).
Contoh 1. Temukan hasil kali vektor yang merupakan vektor-vektor utama dari sistem koordinat siku-siku (Gbr. 156).
1. Karena panjang vektor-vektor utama sama dengan satu satuan skala, maka luas jajar genjang (persegi) secara numerik sama dengan satu. Artinya modulus perkalian vektor sama dengan satu.
2. Karena garis tegak lurus bidang adalah sumbu, maka hasil kali vektor yang diinginkan adalah vektor yang kolinear dengan vektor k; dan karena keduanya memiliki modulus 1, hasil kali vektor yang diinginkan sama dengan k atau -k.
3. Dari dua kemungkinan vektor tersebut, yang pertama harus dipilih, karena vektor k membentuk sistem berarah kanan (dan vektor-vektor bertangan kiri).
Contoh 2. Temukan perkalian silang
Larutan. Seperti pada contoh 1, kita menyimpulkan bahwa vektornya sama dengan k atau -k. Namun sekarang kita harus memilih -k, karena vektor-vektornya membentuk sistem tangan kanan (dan vektor membentuk sistem tangan kiri). Jadi,
Contoh 3. Vektor masing-masing mempunyai panjang 80 dan 50 cm dan membentuk sudut 30°. Dengan menggunakan meter sebagai satuan panjang, tentukan panjang hasil kali vektor a
Larutan. Luas jajar genjang yang dibangun di atas vektor sama dengan Panjang hasil kali vektor yang diinginkan sama dengan
Contoh 4. Tentukan panjang hasil kali vektor dari vektor-vektor yang sama, dengan menggunakan sentimeter sebagai satuan panjang.
Larutan. Karena luas jajar genjang yang dibangun di atas vektor adalah sama, maka panjang hasil kali vektornya adalah 2000 cm, yaitu.
Dari perbandingan contoh 3 dan 4 jelas bahwa panjang vektor tidak hanya bergantung pada panjang faktornya tetapi juga pada pilihan satuan panjang.
Arti fisik dari produk vektor. Dari sekian banyak besaran fisis, diwakili oleh produk vektor, kami hanya mempertimbangkan momen gaya.
Misalkan A adalah titik penerapan gaya. Momen gaya terhadap titik O disebut perkalian vektor, karena modulus perkalian vektor ini secara numerik sama dengan luas jajar genjang (Gbr. 157), maka a adalah titik penerapan gaya. modulus momen sama dengan hasil kali alas dan tinggi, yaitu gaya dikalikan jarak dari titik O ke garis lurus yang dilalui gaya tersebut.
Dalam mekanika terbukti untuk keseimbangan padat Penting agar tidak hanya jumlah vektor yang mewakili gaya-gaya yang diterapkan pada benda sama dengan nol, tetapi juga jumlah momen gaya-gaya tersebut. Dalam kasus dimana semua gaya sejajar pada satu bidang, penjumlahan vektor yang menyatakan momen dapat diganti dengan penjumlahan dan pengurangan besarnya. Tetapi dengan arah kekuatan yang sewenang-wenang, penggantian seperti itu tidak mungkin dilakukan. Sesuai dengan ini, perkalian vektor didefinisikan secara tepat sebagai vektor, dan bukan sebagai bilangan.
Sebelum memberikan konsep perkalian vektor, mari kita beralih ke pertanyaan tentang orientasi rangkap tiga vektor a →, b →, c → dalam ruang tiga dimensi.
Pertama, mari kita sisihkan vektor a → , b → , c → dari satu titik. Orientasi tripel a → , b → , c → bisa ke kanan atau ke kiri, bergantung pada arah vektor c → itu sendiri. Tipe tripel a → , b → , c → ditentukan dari arah putaran terpendek dari vektor a → ke b → dari ujung vektor c → .
Jika putaran terpendek dilakukan berlawanan arah jarum jam, maka tripel vektor a → , b → , c → disebut Kanan, jika searah jarum jam – kiri.
Selanjutnya, ambil dua vektor non-kolinear a → dan b →. Mari kita plot vektor A B → = a → dan AC → = b → dari titik A. Mari kita buat sebuah vektor A D → = c →, yang tegak lurus terhadap A B → dan A C →. Jadi, ketika membangun vektor itu sendiri A D → = c →, kita dapat melakukannya dengan dua cara, yaitu dengan memberikan satu arah atau sebaliknya (lihat ilustrasi).
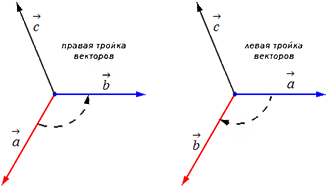
Tripel vektor yang terurut a → , b → , c →, seperti yang telah kita ketahui, dapat berada di kanan atau kiri bergantung pada arah vektornya.
Dari penjelasan di atas kita dapat mengenalkan definisi perkalian vektor. Definisi ini diberikan untuk dua vektor yang didefinisikan dalam sistem koordinat persegi panjang dalam ruang tiga dimensi.
Definisi 1
Hasil kali vektor dua vektor a → dan b → kita akan menyebut vektor yang didefinisikan dalam sistem koordinat persegi panjang ruang tiga dimensi sedemikian rupa sehingga:
- jika vektor a → dan b → segaris, maka vektornya nol;
- itu akan tegak lurus terhadap vektor a → dan vektor b → yaitu. ∠ a → c → = ∠ b → c → = π 2 ;
- panjangnya ditentukan dengan rumus: c → = a → · b → · sin ∠ a → , b → ;
- rangkap tiga vektor a → , b → , c → mempunyai orientasi yang sama dengan sistem koordinat yang diberikan.
Hasil kali vektor dari vektor a → dan b → mempunyai notasi sebagai berikut: a → × b →.
Koordinat hasil kali vektor
Karena setiap vektor mempunyai koordinat tertentu dalam sistem koordinatnya, kita dapat memperkenalkan definisi kedua dari perkalian vektor, yang memungkinkan kita mencari koordinatnya menggunakan koordinat vektor yang diberikan.
Definisi 2
Dalam sistem koordinat persegi panjang ruang tiga dimensi hasil kali vektor dua vektor a → = (a x ; a y ; a z) dan b → = (b x ; b y ; b z) disebut vektor c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , dimana i → , j → , k → adalah vektor koordinat.
Hasil kali vektor dapat direpresentasikan sebagai determinan matriks persegi orde ketiga, dimana baris pertama berisi vektor vektor i → , j → , k → , baris kedua berisi koordinat vektor a → , dan baris ketiga berisi koordinat vektor b → dalam sistem koordinat persegi panjang tertentu, determinan matriksnya seperti ini: c → = a → × b → = i → j → k → a x a y a z b x b y b z
Memperluas determinan ini ke dalam elemen baris pertama, kita memperoleh persamaan: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z · i → - a x a z b x b z · j → + a x a y b x b y · k → = = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →
Sifat-sifat produk silang
Diketahui hasil kali vektor dalam koordinat direpresentasikan sebagai determinan matriks c → = a → × b → = i → j → k → a x a y a z b x b y b z , maka atas dasar sifat-sifat determinan matriks berikut ini ditampilkan sifat-sifat produk vektor:
- antikomutatif a → × b → = - b → × a → ;
- distributivitas a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → atau a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
- asosiatifitas λ a → × b → = λ a → × b → atau a → × (λ b →) = λ a → × b →, dengan λ adalah bilangan real sembarang.
Properti ini memiliki bukti sederhana.
Sebagai contoh, kita dapat membuktikan sifat antikomutatif suatu perkalian vektor.
Bukti antikomutatif
Berdasarkan definisi, a → × b → = i → j → k → a x a y a z b x b y b z dan b → × a → = i → j → k → b x b y b z a x a y a z . Dan jika dua baris matriks tersebut ditukar, maka nilai determinan matriks tersebut akan berubah menjadi kebalikannya, maka a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x a y a z = - b → × a → , yang membuktikan bahwa hasil kali vektor bersifat antikomutatif.
Produk vektor - contoh dan solusi
Dalam kebanyakan kasus, ada tiga jenis masalah.
Dalam soal tipe pertama, panjang dua vektor dan sudut di antara keduanya biasanya diberikan, dan Anda perlu mencari panjang hasil kali vektor. Dalam hal ini mereka menggunakan rumus berikut c → = a → b → dosa ∠ a → , b → .
Contoh 1
Carilah panjang hasil kali vektor dari vektor a → dan b →, jika diketahui a → = 3, b → = 5, ∠ a →, b → = π 4.
Larutan
Dengan menentukan panjang hasil kali vektor dari vektor a → dan b → kita menyelesaikannya tugas yang diberikan: a → × b → = a → · b → · sin ∠ a → , b → = 3 · 5 · sin π 4 = 15 2 2 .
Menjawab: 15 2 2 .
Soal tipe kedua mempunyai hubungan dengan koordinat vektor, di dalamnya hasil kali vektor, panjangnya, dll. dicari melalui koordinat yang diketahui dari vektor tertentu a → = (ax; ay; az) Dan b → = (b x ; b y ; b z) .
Untuk jenis masalah ini, Anda dapat menyelesaikan banyak pilihan tugas. Misalnya, koordinat vektor a → dan b → tidak dapat ditentukan, tetapi perluasannya menjadi vektor koordinat berbentuk b → = b x · saya → + b y · j → + b z · k → dan c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →, atau vektor a → dan b → dapat ditentukan dengan koordinat awalnya dan titik akhir.
Perhatikan contoh berikut.
Contoh 2
Dalam sistem koordinat persegi panjang, diberikan dua vektor: a → = (2; 1; - 3), b → = (0; - 1; 1). Temukan produk silangnya.
Larutan
Menurut definisi kedua, kita mencari perkalian vektor dari dua vektor di koordinat yang diberikan: a → × b → = (a y · b z - a z · b y) · i → + (az · b x - a x · b z) · j → + (ax · b y - a y · b x) · k → = = (1 · 1 - (- 3) (- 1)) i → + ((- 3) 0 - 2 1) j → + (2 (- 1) - 1 0) k → = = - 2 i → - 2 j → - 2k → .
Jika kita menuliskan hasil kali vektor dalam bentuk determinan matriks, maka penyelesaiannya contoh ini terlihat seperti ini: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 = - 2 i → - 2 j → - 2 k → .
Menjawab: a → × b → = - 2 saya → - 2 j → - 2 k → .
Contoh 3
Tentukan panjang hasil kali vektor dari vektor i → - j → dan i → + j → + k →, dengan i →, j →, k → adalah vektor satuan dari sistem koordinat kartesius persegi panjang.
Larutan
Pertama, cari koordinat hasil kali vektor i → - j → × i → + j → + k → dalam sistem koordinat persegi panjang tertentu.
Diketahui vektor i → - j → dan i → + j → + k → berturut-turut mempunyai koordinat (1; - 1; 0) dan (1; 1; 1). Mari kita cari panjang hasil kali vektor menggunakan determinan matriks, maka kita mempunyai i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2 k → .
Oleh karena itu, hasil kali vektor i → - j → × i → + j → + k → memiliki koordinat (- 1 ; - 1 ; 2) pada sistem koordinat yang diberikan.
Kita mencari panjang hasil kali vektor menggunakan rumus (lihat bagian mencari panjang vektor): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6.
Menjawab: saya → - j → × saya → + j → + k → = 6 . .
Contoh 4
Dalam sistem koordinat kartesius persegi panjang, diberikan koordinat tiga titik A (1, 0, 1), B (0, 2, 3), C (1, 4, 2). Temukan beberapa vektor yang tegak lurus A B → dan A C → secara bersamaan.
Larutan
Vektor A B → dan A C → masing-masing mempunyai koordinat sebagai berikut (- 1 ; 2 ; 2) dan (0 ; 4 ; 1). Setelah menemukan hasil kali vektor dari vektor A B → dan A C →, jelaslah bahwa itu benar vektor tegak lurus menurut definisinya, untuk A B → dan AC →, yaitu, ini adalah solusi untuk masalah kita. Mari kita cari A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → .
Menjawab: - 6 saya → + j → - 4 k → . - salah satu vektor tegak lurus.
Masalah tipe ketiga difokuskan pada penggunaan sifat-sifat perkalian vektor dari vektor. Setelah menerapkannya, kita akan mendapatkan solusi dari masalah yang diberikan.
Contoh 5
Vektor a → dan b → tegak lurus dan panjangnya masing-masing 3 dan 4. Tentukan panjang hasil kali vektor 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → .
Larutan
Berdasarkan sifat distributif suatu perkalian vektor, kita dapat menuliskan 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →
Berdasarkan sifat asosiatif, kita mengambil koefisien numerik dari tanda perkalian vektor pada ekspresi terakhir: 3 · a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → = = 3 · a → × a → + 3 · (- 2) · a → × b → + (- 1) · b → × a → + (- 1) · (- 2) · b → × b → = = 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b →
Hasil kali vektor a → × a → dan b → × b → sama dengan 0, karena a → × a → = a → · a → · sin 0 = 0 dan b → × b → = b → · b → · sin 0 = 0, lalu 3 · a → × a → - 6 · a → × b → - b → × a → + 2 · b → × b → = - 6 · a → × b → - b → × a → . .
Dari antikomutatifitas perkalian vektor diperoleh - 6 · a → × b → - b → × a → = - 6 · a → × b → - (- 1) · a → × b → = - 5 · a → × b → . .
Dengan menggunakan sifat-sifat hasil kali vektor, kita memperoleh persamaan 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → .
Dengan syarat, vektor a → dan b → tegak lurus, yaitu sudut antara keduanya sama dengan π 2. Sekarang yang tersisa hanyalah mengganti nilai yang ditemukan ke dalam rumus yang sesuai: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → · sin (a → , b →) = 5 · 3 · 4 · sin π 2 = 60 .
Menjawab: 3 a → - b → × a → - 2 b → = 60.
Panjang hasil kali vektor vektor menurut definisi sama dengan a → × b → = a → · b → · sin ∠ a → , b → . Karena sudah diketahui (dari kursus sekolah) bahwa luas segitiga sama dengan setengah hasil kali panjang kedua sisinya dikalikan sinus sudut antara sisi-sisi tersebut. Oleh karena itu, panjang hasil kali vektor sama dengan luas jajar genjang - segitiga berlipat ganda, yaitu hasil kali sisi-sisinya yang berupa vektor a → dan b →, diletakkan dari satu titik, dengan sinus dari sudut antara keduanya sin ∠ a →, b →.
Inilah arti geometris dari perkalian vektor.
Arti fisik dari produk vektor
Dalam mekanika, salah satu cabang fisika, berkat perkalian vektor, Anda dapat menentukan momen suatu gaya relatif terhadap suatu titik dalam ruang.
Definisi 3
Berdasarkan momen gaya F → yang diterapkan pada titik B, relatif terhadap titik A, kita akan memahami hasil kali vektor berikut A B → × F →.
Jika Anda melihat kesalahan pada teks, sorot teks tersebut dan tekan Ctrl+Enter
