Bilangan kompleks dalam ujian. Kemungkinan menggunakan bilangan kompleks dalam kursus matematika sekolah menengah. Kemampuan untuk menggunakan bilangan kompleks

KEMUNGKINAN MENGGUNAKAN ANGKA KOMPLEKS

PADA KURSUS MATEMATIKA DI SEKOLAH PENDIDIKAN UMUM

Penasihat ilmiah:

Institusi pendidikan kota

Sekolah menengah Pervomaiskaya

Dengan. Kota Kichmengsky

St. Zarechnaya 38

Karya yang disajikan dikhususkan untuk penelitian bilangan kompleks. Relevansi: menyelesaikan banyak masalah dalam fisika dan teknologi mengarah pada persamaan kuadrat dengan diskriminan negatif. Persamaan ini tidak mempunyai solusi dalam domain bilangan real. Namun solusi dari banyak masalah seperti itu mempunyai arti fisik yang sangat pasti.

Signifikansi praktis: bilangan kompleks dan fungsi variabel kompleks digunakan dalam banyak masalah sains dan teknologi, dan dapat digunakan di sekolah untuk menyelesaikan persamaan kuadrat.

Daerah objek: matematika. Objek penelitian: konsep aljabar dan tindakan. Subyek penelitian- bilangan kompleks. Masalah: bilangan kompleks tidak diajarkan dalam mata kuliah matematika sekolah Menengah, meskipun dapat digunakan untuk menyelesaikan persamaan kuadrat. Kemungkinan memasukkan bilangan kompleks ke dalam Tugas Ujian Negara Bersatu di masa depan. Hipotesa: Anda dapat menggunakan bilangan kompleks untuk menyelesaikan persamaan kuadrat di sekolah menengah. Target: untuk mempelajari kemungkinan penggunaan bilangan kompleks ketika belajar matematika di kelas 10 sekolah menengah. Tugas: 1. Mempelajari teori bilangan kompleks 2. Pertimbangkan kemungkinan penggunaan bilangan kompleks dalam mata pelajaran matematika kelas 10. 3. Mengembangkan dan menguji tugas-tugas dengan bilangan kompleks.

Untuk solusi persamaan aljabar Jumlah bilangan riil tidak cukup. Oleh karena itu, wajar jika kita berusaha membuat persamaan ini dapat dipecahkan, yang pada gilirannya akan mengarah pada perluasan konsep bilangan..gif" width="10" height="65 src=">

https://pandia.ru/text/78/027/images/image005_18.gif" width="10" height="62">.gif" width="97" height="28 src=">

Anda hanya perlu setuju untuk bertindak berdasarkan ekspresi tersebut sesuai dengan aturan aljabar biasa dan berasumsi demikian

Pada tahun 1572, buku aljabar Italia R. Bombelli diterbitkan, di mana aturan pertama ditetapkan operasi aritmatika atas angka-angka tersebut, hingga mengekstraksi akar pangkat tiga darinya. Nama “bilangan imajiner” diperkenalkan pada tahun 1637. Matematikawan Perancis dan filsuf R. Descartes, dan pada tahun 1777 salah satu matematikawan terhebat abad ke-8 X..gif" width="58" height="19"> sebagai contoh penggunaan bilangan kompleks dalam pembelajaran matematika di kelas 10. Oleh karena itu, bilangan x yang kuadratnya –1 disebut satuan imajiner dan dilambangkan dengan i ="100" height="27 src=" >kelas 8" href="/text/category/8_klass/" rel="bookmark">kelas 8 aljabar. - M.: Pendidikan, 1994.-P.134- 139.

2. kamus ensiklopedis matematikawan muda/ Komp. E-68. - M.: Pedagogi, 19c

Teks bagian dari publikasi

Isi
Pendahuluan………………………………………………………………………..3 Bab I. Dari Sejarah Bilangan Kompleks…………………………… ……………………… ............4 Bab II. Dasar-dasar metode bilangan kompleks……………………………………6 Bab III. Geometri segitiga bilangan kompleks…………………......12 Bab IV. Larutan Masalah Ujian Negara Bersatu dan berbagai olimpiade dengan menggunakan metode bilangan kompleks……………………………………………………………....20 Kesimpulan…………………………… ……… ………………………………….24 Daftar Pustaka………………………………………………………………..25

Perkenalan
Pentingnya bilangan kompleks dalam matematika dan penerapannya telah diketahui secara luas. Aljabar bilangan kompleks dapat berhasil digunakan dalam geometri dasar, trigonometri, teori gerak dan persamaan, serta dalam teknik elektro, berbagai mekanika dan masalah fisik. Dalam planimetri, metode bilangan kompleks memungkinkan Anda menyelesaikan masalah dengan perhitungan langsung menggunakan rumus yang sudah jadi. Inilah kesederhanaan metode ini dibandingkan dengan vektor dan metode koordinat, dengan metode transformasi geometri, menuntut siswa memiliki kecerdasan yang cukup dan pencarian yang panjang. Selama beberapa milenium, segitiga telah menjadi simbol geometri. Anda bahkan dapat mengatakan bahwa segitiga adalah atom geometri. Poligon apa pun dapat dibagi menjadi segitiga, dan studi tentang sifat-sifatnya direduksi menjadi mempelajari sifat-sifat segitiga komponen-komponennya. Mari kita lihat cara kerja metode bilangan kompleks saat membuktikan sifat-sifat segitiga kursus sekolah planimetri, serta untuk menyelesaikan soal C-4 UN Unified State. 2

Bab I. Dari Sejarah Bilangan Kompleks,,
Rupanya, untuk pertama kalinya besaran imajiner disebutkan dalam karya terkenal “Great Art, or About aturan aljabar» Cardano (1545), sebagai bagian dari solusi formal masalah penghitungan dua bilangan yang berjumlah 10 dan jika dikalikan menghasilkan 40. Untuk soal ini, ia memperoleh persamaan kuadrat untuk salah satu suku, dan menemukan akar-akarnya: 5 + √ − 15 dan 5 − √ − 15 . Dalam komentarnya terhadap solusi tersebut, ia menulis: “kuantitas yang paling kompleks ini tidak berguna, meskipun sangat cerdik” dan “Pertimbangan aritmatika menjadi semakin sulit dipahami, mencapai batas yang halus sekaligus tidak berguna.” Kemungkinan menggunakan besaran imajiner ketika menyelesaikan persamaan kubik, dalam apa yang disebut kasus tak tersederhanakan (ketika akar real dari polinomial dinyatakan melalui akar kubus besaran imajiner), pertama kali dijelaskan oleh Bombelli (1572). Dia adalah orang pertama yang mendeskripsikan aturan penjumlahan, pengurangan, perkalian dan pembagian bilangan kompleks, namun tetap menganggapnya sebagai “penemuan” yang tidak berguna dan licik. Ekspresi yang dapat direpresentasikan dalam bentuk a + b √ − 1, muncul saat menyelesaikan kuadrat dan persamaan kubik, mulai disebut "imajiner" di abad XVI-XVII atas dorongan Descartes, yang menyebut mereka demikian, menolak realitasnya, dan bagi banyak ilmuwan besar lainnya di abad ke-17, sifat dan hak keberadaan besaran imajiner tampak sangat diragukan, sama seperti mereka dianggap meragukan pada saat itu. bilangan irasional, dan bahkan nilai negatif. Meskipun demikian, para ahli matematika dengan berani menerapkan metode formal aljabar besaran nyata ke besaran kompleks, memperoleh hasil nyata yang benar bahkan dari besaran menengah yang kompleks, dan ini mulai membangkitkan kepercayaan diri. Untuk waktu yang lama, tidak jelas apakah semua operasi pada bilangan kompleks menghasilkan hasil yang kompleks atau nyata, atau apakah, misalnya, mengekstraksi akar dapat menghasilkan penemuan jenis bilangan baru. Soal menyatakan akar-akar derajat n dari nomor yang diberikan diselesaikan dalam karya Moivre (1707) dan Cotes (1722). Simbol untuk menunjukkan satuan imajiner dikemukakan oleh Euler (1777, diterbitkan 1794), yang mengambil huruf pertama dari kata Latin untuk ini. imaginarius - imajiner. Dia juga memperluas semua fungsi standar, termasuk logaritma, ke domain kompleks. Euler juga mengungkapkan gagasannya pada tahun 1751 bahwa bidang bilangan kompleks tertutup secara aljabar. D'Alembert (1747) sampai pada kesimpulan yang sama, tetapi bukti kuat pertama dari fakta ini adalah milik Gauss (1799). Gauss-lah yang menciptakan istilah "bilangan kompleks" dan digunakan secara luas pada tahun 1831, meskipun istilah tersebut sebelumnya telah digunakan dalam pengertian yang sama oleh ahli matematika Perancis Lazare Carnot pada tahun 1803. 3
Model aritmatika (standar) bilangan kompleks sebagai pasangan bilangan real dibangun oleh Hamilton (1837); ini membuktikan konsistensi sifat-sifatnya. Jauh sebelumnya, pada tahun 1685, dalam karyanya “Aljabar,” Wallis (Inggris) menunjukkan hal itu akar yang kompleks persamaan kuadrat dengan koefisien nyata dapat direpresentasikan secara geometris, dengan titik-titik pada bidang. Tapi hal itu luput dari perhatian. Kali berikutnya interpretasi geometris bilangan kompleks dan operasinya muncul dalam karya Wessel (1799). Representasi geometris modern, kadang-kadang disebut “diagram Argand”, mulai digunakan setelah publikasi karya J. R. Argand pada tahun 1806 dan 1814, yang secara independen mengulangi kesimpulan Wessel. Istilah “modulus”, “argumen”, dan “bilangan konjugat” diperkenalkan oleh Cauchy. Dengan demikian, ditemukan bahwa bilangan kompleks juga cocok untuk melakukan operasi aljabar murni penjumlahan, pengurangan, perkalian dan pembagian vektor pada bidang, yang sangat mengubah aljabar vektor. 4

Bab II. Dasar-dasar Metode Bilangan Kompleks
[ 1 ]
,
[2], [3] [4] Penafsiran geometris bilangan kompleks Panjang suatu ruas Diberikan persegi panjang sistem kartesius koordinat pada bidang, bilangan kompleks z = x+iy (i 2 = -1) dapat diasosiasikan satu-satu dengan titik M bidang dengan koordinat x, y (Gbr. 1): z = x + iy ↔M (x, y ) ↔M (z) . Bilangan z kemudian disebut koordinat kompleks titik M. Karena himpunan titik-titik pada bidang Euclidean berkorespondensi satu-satu dengan himpunan bilangan kompleks, maka bidang ini disebut juga bidang bilangan kompleks. Titik asal O sistem koordinat Kartesius disebut titik awal atau titik nol pada bidang bilangan kompleks. Bila = 0 bilangan z real. Bilangan real dilambangkan dengan titik-titik pada sumbu x, oleh karena itu disebut sumbu real. Pada x=0, bilangan z murni khayalan: z=iy. Angka imajiner diwakili oleh titik-titik pada sumbu y, oleh karena itu disebut sumbu imajiner. Nol adalah bilangan nyata dan bilangan imajiner murni. Jarak dari titik awal bidang O ke titik M(z) disebut modulus bilangan kompleks z dan dilambangkan dengan |z| atau r: | z | = r = | OM | = √ x 2 + y 2 Jika φ adalah sudut orientasi yang dibentuk oleh vektor ⃗ OM dengan sumbu x, maka menurut definisi fungsi sinus dan cosinus sin φ = y r, cos φ = x r 5
dimana x = r cos φ, y = r sin φ, dan oleh karena itu z = r (cos φ + sin φ). Representasi bilangan kompleks z ini disebut nya
trigonometri

cheskoe
membentuk.
Representasi asli z=x+iy disebut
aljabar
bentuk nomor ini. Dalam representasi trigonometri, sudut  disebut argumen bilangan kompleks dan dinotasikan juga dengan arg z: φ = arg z Jika diberikan bilangan kompleks z = x + iy, maka bilangan ´ z = x − iy disebut
konjugat kompleks
(atau sederhananya
mengkonjugasikan
) ke nomor ini z. Maka jelaslah bilangan z juga terkonjugasi dengan bilangan ´ z. Titik M(z) dan M 1 (´ z) simetris terhadap sumbu x. Dari persamaan z = ´ z maka y = 0 dan sebaliknya. Artinya

angka yang sama dengan
konjugatnya adalah nyata dan sebaliknya.
Titik dengan koordinat kompleks z dan -z simetris terhadap titik awal O. Titik dengan koordinat kompleks z dan − ´ z simetris terhadap sumbu y. Dari persamaan z = ´ z maka x = 0 dan sebaliknya. Oleh karena itu, kondisi z =− ´ z adalah kriteria bilangan imajiner murni. Untuk nomor z apa pun, tentu saja | z | = | ´ z | =¿− z ∨¿∨−´ z ∨¿ .
Jumlah dan produk
bilangan, berturut-turut, adalah jumlah, hasil kali, atau hasil bagi bilangan yang dikonjugasikan ke bilangan kompleks tertentu: ´ z 1 + z 2 = ´ z 1 + ´ z 2 ; ´ z 1 z 2 = ´ z 1 ´ z 2 ; ´ z 1: z 2 = ´ z 1: ´ z 2 Persamaan ini dapat dengan mudah diverifikasi menggunakan rumus operasi bilangan kompleks. Jika a dan b - koordinat yang kompleks titik A dan B berturut-turut, maka bilangan c = a + b adalah koordinat titik C, sehingga ⃗ OC = ⃗ OA + ⃗ OB (Gbr. 3). Bilangan kompleks d = a − b bersesuaian dengan titik D sehingga ⃗ OD = ⃗ OA − ⃗ OB . Jarak antara titik A dan B adalah | ⃗BA | = | ⃗ OD | =¿ a − b ∨¿: ¿ AB ∨¿∨ a − b ∨¿ (1) Karena ¿ z ∨ 2 = z ´ z , maka ¿ AB ∨ 2 =(a − b) (´ a − ´ b) . (2)
Persamaannya
z ´ z = r 2
mendefinisikan lingkaran dengan pusat

Tentang radius

R.
Hubungan AC CB = λ, (λ ≠ − 1), di mana titik C membagi suatu segmen AB, dinyatakan melalui koordinat kompleks titik-titik ini sebagai berikut: λ = c − a b − c, λ = ´ λ, dengan demikian c = a + λb 1 + λ (3) Jika λ = 1, titik C adalah titik tengah ruas AB, dan sebaliknya. Maka: c = 1 2 (a + b) (4) Perkalian bilangan kompleks Perkalian bilangan kompleks dilakukan sesuai rumus, Yaitu | ab | = | sebuah || b | , dan 7
Paralelisme dan tegak lurus Kolinearitas tiga titik Misalkan titik A(a) dan B(b) diberikan pada bidang bilangan kompleks. Vektor ⃗ OA dan ⃗ OB berarah bersama jika dan hanya jika arg a = arg b, yaitu ketika arg a – arg b=arg a b =0 (saat membagi bilangan kompleks, argumen pembagi dikurangi dari argumen bilangan kompleks dividen). Jelas juga bahwa vektor-vektor ini mempunyai arah yang berlawanan jika dan hanya jika arg a - arg b= arg a b = ± π. Bilangan kompleks dengan argumen 0, π, - π adalah bilangan real.
Kriteria kolinearitas titik O, A, B:
Agar titik A(a) dan B(b) segaris dengan titik awal O, maka hasil bagi a b harus sama dengan bilangan real, yaitu a b = ´ a ´ b atau a ´ b = ´ a b (6) Sekarang ambil poin A(a), B(b), C(c), D(d). Vektor ⃗ BA dan ⃗ DC collie adalah non-ary jika dan hanya jika titik-titiknya didefinisikan oleh kompleks angka a-b dan с-d, segaris dengan permulaan O. Catatan: 1. Berdasarkan (6) kita peroleh: ⃗ AB ∨¿ ⃗ CD↔ (a − b) (´ c − ´ d) =(´ a − ´ b ) (c − d) ; (8) 2. Jika titik A, B, C, D termasuk dalam lingkaran satuan z ´ z = 1, maka ´ a = 1 a; ´ b = 1 b ; ´ c = 1 c ; ´ d = 1 d dan oleh karena itu kondisi (8) berbentuk: ⃗ AB ∨¿ ⃗ CD↔ ab = cd ; (9) 3. Kolinearitas titik A, B, C dicirikan oleh kolinearitas vektor ⃗AB dan ⃗AC. Dengan menggunakan (8), kita peroleh: (a − b) (´ a −´ c) =(´ a − ´ b) (a − c) (10) Ini adalah kriteria agar titik A, B, C berada ke garis lurus yang sama. Dapat direpresentasikan dalam bentuk simetris a (´ b −´ c) + b (´ c −´ a) + c (´ a − ´ b) = 0 (11) 8
Jika titik A dan B termasuk dalam lingkaran satuan z ´ z = 1, maka ´ a = 1 a; ´ b = 1 b dan oleh karena itu masing-masing relasi (10) dan (11) ditransformasikan (setelah dikurangi (a-b) menjadi berikut: c + ab ´ c = a + b (12) Titik A dan B adalah tetap, dan intinya Kita akan menganggap C sebagai variabel, menentukan ulang koordinatnya dengan z. Maka masing-masing relasi yang diperoleh (10), (11), (12) akan menjadi persamaan garis lurus AB: (´ a − ´ b) z + (b − a) ´ z + a ´ b − b ´ a = 0 , (10a) z + ab ´ z = a + b a z . Oleh karena itu, OA ⊥ OB↔ a b = − ´ a ´ b atau OA ⊥ OB↔a ´ b + ´ a b = 0 (13) Tegak lurus segmen AB dan CD ditentukan oleh persamaan (a − b) (´ c − ´ d) + (´ a − ´ b) (c − d) = 0 (14) Khususnya, jika titik A, B, C, D termasuk dalam lingkaran satuan z ´ z = 1 , maka ketergantungan (14) disederhanakan: ab + cd = 0 (15) Produk skalar vektor dinyatakan. produk skalar vektor ⃗ OA dan ⃗ OB melalui koordinat kompleks a dan b dari titik A dan B. Misal a=x 1 +iy 1 , b=x 2 +iy 2 . Maka a b + a b=(x 1 +iy 1)(x 2 −iy 2)+(x 1 −iy 1)(x 2 +iy 2)=2(x 1 x 2 +y 1 y 2)= 2 ⃗ OA∙⃗OB. Jadi, ⃗ OA ∙ ⃗ OB = 1 2 (a b + ab) (16) 9
Biarlah sekarang empat diberikan poin sewenang-wenang A(a), B(b), C(c), D(d) dengan koordinat kompleksnya. Maka 2 ⃗ AB ∙ ⃗ CB = 1 2 (a-b)(c - d)+(a - b)(c-d) (17) Sudut Mari kita sepakat untuk menyatakan dengan simbol ∠ (AB ,CD) sudut yang berorientasi positif melalui yang mana vektor ⃗ harus diputar AB agar searah dengan vektor ⃗ CD. Maka, cos ∠ (AB, CD)= (d − c) (´ b − ´ a) +(´ d −´ c)(b − a) 2 | d − c || b− a | (18) sin ∠ (AB ,CD)= (d − c) (´ b −´ a) +(´ d −´ c)(b − a) 2 i | d − c || b− a | (19) Titik potong garis potong lingkaran Jika titik A, B, C dan D terletak pada lingkaran z ´ z = 1, maka koordinat kompleks titik potong tersebut dicari dengan rumus ´ z = (a + b) − (c + d) ab − cd (20) Jika AB tegak lurus CD, maka z= 1 2 (a+b+c+d) (21) Titik potong garis singgung lingkaran 10
Koordinat kompleks titik potong garis singgung lingkaran z ´ z =1 di titik A(a) dan B(b) ditentukan dengan rumus z= 2ab a + b (22) Proyeksi ortogonal suatu titik pada garis lurus Proyeksi ortogonal suatu titik M(m) pada garis lurus AB, dimana A(a) dan B(b) ditentukan dengan rumus Jika A dan B termasuk dalam lingkaran satuan z= 1 2 (a + b + m − cb m) .
Bab III.

Geometri segitiga dalam bilangan kompleks
Pada bidang bilangan kompleks, sebuah segitiga ditentukan oleh tiga bilangan kompleks yang bersesuaian dengan titik sudutnya. Centroid dan orthocenter suatu segitiga. [ 2 ] Diketahui bahwa untuk pusat massa G (titik potong median) segitiga ABC dan sembarang titik O persamaan berikut ini benar: ⃗ OG = 1 3 (⃗ OA + ⃗ OB + ⃗ OC). Oleh karena itu, koordinat kompleks g dari pusat massa G dihitung dengan rumus g = 1 3 (a + b + c) (23) Mari kita nyatakan h koordinat kompleks ortocenter H segitiga ABC melalui koordinat a, b, c dari simpulnya. Misalkan garis AH, BH, CH memotong lingkaran luar segitiga berturut-turut di titik A1, B1, C1. Misalkan lingkaran ini mempunyai persamaan z ´ z =1, maka berdasarkan (15) kita mempunyai: a 1 = − b c a , b 1 = − ca b , c 1 = − ab c Dengan rumus (20) h = (a + a 1 ) −(b + b 1) a a 1 − bb 1 = ab + bc + ca abc = 1 a + 1 b + 1 c 11
Darimana h=a+b+c berasal. (24) Persamaan yang dihasilkan memuat koordinat titik-titik sudut segitiga secara simetris, oleh karena itu tinggi ketiga segitiga tersebut melalui titik potong dua segitiga pertama. Segitiga sebangun [2,1] Segitiga ABC dan A 1 B 1 C 1 Sebangun dan berorientasi identik (kesamaan jenis pertama), jika B 1 =kAB, A 1 B 1 =kAC dan sudut B 1 A 1 C 1 dan BAC sama besar (sudut-sudutnya berorientasi). Dengan menggunakan bilangan kompleks, persamaan tersebut dapat ditulis sebagai berikut: |a 1 −b 1 |=k|a−b|, |a 1 −c 1 |=k|a−c|,arg c 1 − a 1 b 1 − a 1 =arg c − a b − a . Kedua persamaan tersebut setara dengan satu dengan 1 − a 1 c − a = b 1 − a 1 b − a = σ , (25) dengan σ adalah bilangan kompleks, |σ|=k-koefisien kemiripan. Jika σ real, maka c 1 − a 1 c − a = ´ c 1 − ´ a 1 ´ c − ´ a , dengan AC║A 1 C 1. Oleh karena itu, segitiga ABC dan A 1 B 1 C 1 bersifat homotetis. Relasi (25) diperlukan dan kondisi cukup sehingga segitiga ABC dan A 1 B 1 C 1 sebangun dan berorientasi sama. Dapat diberi bentuk simetris ab 1 +bc 1 +ca 1 =ba 1 +cb 1 +ac 1 (25a) Segitiga sama kaki Jika | σ | = 1, maka segitiga ABC dan A 1 B 1 C 1 sama besar. Maka relasi (25) adalah tanda persamaan segitiga-segitiga yang orientasinya sama, dan relasi (26) adalah tanda persamaan segitiga-segitiga yang orientasinya berlawanan. Segitiga beraturan Jika Anda memerlukan orientasi segitiga ABC sebangun dengan segitiga BCA, maka segitiga ABC beraturan. 12
Oleh karena itu, dari (25) kita peroleh syarat perlu dan cukup agar segitiga ABC beraturan (a−b) 2 +(b−c) 2 +(c−a) 2 =0 (27) Luas segitiga (dibuktikan oleh penulis) Kita peroleh rumus luas S segitiga berorientasi positif ABC: S = 1 2 | AB || AC | sin ∠ (AB , AC)= 1 4i ((c − a) (´ b − ´ a) − (b − a) (´ c − ´ a)) = − 1 4i (a (´ b − ´ c) + b (´ c − ´ a) + c (´ a − ´ b)) atau S = i 4 (a (´ b − ´ c) + b (´ c − ´ a) + c (´ a − ´ b )) (28) Jika segitiga ABC pada lingkaran z ´ z = 1, maka rumus (28) diubah menjadi bentuk: S = i 4 (a − b)(b − c)(c − a) abc (29) Teorema tentang garis tengah a segitiga (dibuktikan oleh penulis)
Dalil
. garis tengah segitiga tersebut sejajar dengan alasnya dan sama dengan setengah alasnya. Bukti. Misalkan titik M dan N adalah titik tengah sisi AB dan BC, maka m = b 2 ; n = b + c 2 . Karena z 2 =z ´ z, maka MN 2 =(m-n)(´ m - ´ n)=(b 2 - b + c 2)(´ b 2 – ´ b + ´ c 2)= b ´ b 4 − b ´ b + b ´ c 4 − b ´ b + ´ b c 4 + b ´ b + b ´ c + ´ b c + c ´ c 4 = c ´ c 4 13
4MN 2 =c ´ c, AC 2 =(c-0)(c-0)=c ´ c, maka 4MN 2 = AC 2 atau 2MN=AC.Kondisi (8) kolinearitas vektor MN dan AC juga terpenuhi , dan karenanya MN ║AC. Teorema Thales (dibuktikan oleh penulis)
Dalil
. Jika pada salah satu sisi suatu sudut terdapat garis-garis sejajar yang memotong ruas-ruas yang sama besar, maka pada sisi yang lain garis-garis itu memotong ruas-ruas yang sama besar. Bukti Mari kita asumsikan bahwa c=kb. Lalu jika BD||CE, maka kita punya (b-d)(´ c − 2 ´ d ¿= (´ b − ´ d) (c − 2d) Membuka tanda kurung dan membawa istilah serupa, kita peroleh persamaan b ´ c − 2 b ´ d −´ c d = ´ b c − 2 ´ b d − c ´ d Mengganti c dengan kb dan ´ c dengan k ´ b , kita mendapatkan bk ´ b -2b ´ d -dk ´ b = ´ b kb-2 ´ b d-kb ´ d . Membawa kembali suku-suku serupa dan memindahkan semuanya ke satu sisi, kita mendapatkan 2b ´ d + dk ´ b − 2 ´ b d − kb ´ d =0. Kami akan mengeluarkannya pengganda umum dan kita mendapatkan 2(b ´ d − ´ b d ¿+ k (´ b d − b ´ d) = 0. Maka k=2, yaitu c=2b. Demikian pula, dibuktikan bahwa f=3b, dst. Teorema Pythagoras ( dibuktikan oleh penulis) B segitiga siku-siku kuadrat sisi miring sama dengan jumlahnya kaki persegi 14
Bukti. Jarak antara titik B dan C sama dengan BC=|b-c|=b, BC 2 =b ´ b. Sejak |z| 2 = z ´ z , maka AC 2 =(a-c)(c ´ a − ´ ¿ ¿=(a − 0) (´ a - 0)=a ´ a . AB 2 =(a-b)(´ a − ´ b ¿= a ´ a − a ´ b - ´ a b+b ´ b. Karena b adalah bilangan real, yaitu b= ´ b , maka -a ´ b =− ab a, yaitu - ´ ab = ab. Jadi, AB 2 = a ´ a -a ´ b - ´ ab +b ´ b = a ´ a +b ´ b = AC 2 +BC 2. Teorema Euler terbukti garis lurus (dibuktikan oleh penulis) Mari kita buktikan bahwa ortocenter, centroid dan sirkumcenter segitiga terletak pada satu garis lurus yang sama (garis lurus ini disebut garis lurus Euler), dan OG = 1/2GH 15.
Bukti: Titik G(g) adalah titik berat segitiga ABC, H(h) adalah ortosenternya, dan O(o) adalah pusat lingkaran luar segitiga tersebut. Agar titik-titik ini segaris, persamaan (10) harus dipenuhi: (g-о)(´ g - ´ h ¿ -(´ g − ´ o ¿ (g − h) =0 Mari kita ambil titik O sebagai titik asal, maka g(´ g - ´ h ¿ - ´ g (g − h) =g 2 -g ´ h −¿ (g 2 - h ´ g ¿ =-g ´ h + h ´ g (30) koordinat kompleks ortosenter dihitung dengan rumus (24) h=a+b+c, (30a) dan titik berat massa menurut rumus (23) g = 1 3 (a + b + c) (30c) Substitusikan ke dalam ( 30), kita mendapatkan 1 3 (a+b +c)(´ a + b + c)-(a+b+c)(´ a + b + c 1 3 ¿))=0 Oleh karena itu, titik berat, ortopusat, dan pusat segitiga berbatas terpenuhi. OG=g= 1 3 (a+b+c) GH=h-g=a+b+c- 1 3 (a +b+c)= 2 3 (a+b+c) Didapatkan bahwa OG= 1 2 GH. Teorema tersebut terbukti 16.
Lingkaran Euler (lingkaran sembilan titik). Dibuktikan oleh penulis Perhatikan segitiga ABC. Mari kita sepakat bahwa‌ | OA | = | OB | = | oke | =1, yaitu semua titik sudut segitiga termasuk dalam lingkaran satuan z ´ z = 1 (pusat lingkaran luar O adalah titik asal, dan jari-jari adalah satuan panjang). Mari kita buktikan bahwa alas tiga ketinggian segitiga sembarang, titik tengah ketiga sisinya, dan titik tengah tiga ruas yang menghubungkan titik sudutnya dengan ortosenter terletak pada lingkaran yang sama, dan pusatnya adalah titik tengah ruas OH , di mana H, ingat, adalah ortocenter segitiga ABC. Lingkaran seperti ini disebut
lingkaran Euler
. Misalkan titik K, L dan M adalah titik tengah sisi-sisi segitiga ABC, titik Q, N, P adalah alas ketinggiannya, titik F, E, D adalah titik tengah tiga ruas yang menghubungkan titik sudutnya dengan ortosenter. Mari kita buktikan bahwa titik D, E, F, K, L, M, N, P, Q berada pada lingkaran yang sama. Tetapkan koordinat kompleks yang bersesuaian pada titik-titik tersebut: k = a + b 2 , l = b + c 2 ; m = a + c 2 ,o 1 = h 2 = a + b + c 2 d = 2a + b + c 2 ; e = 2 c + a + b 2 ; f = 2 b + a + c 2 n = 1 2 (a + b + c − ab c) , q = 1 2 (a + c + b − ac b) , p = 1 2 (c + b + a − cb a) O 1 K = | o 1 − k | = | c 2 | ,O 1 L = | o 1 − aku | = | sebuah 2 | , HAI 1 M = | o 1 − m | = | b 2 | HAI 1 D = | o 1 − d | = | sebuah 2 | ,O 1 E = | o 1 − e | = | c 2 | ,O 1 F = | o 1 − f | = | b 2 | HAI 1 N= | o 1 − n | = 1 2 | ab c | = 1 2 | sebuah || b | | c | , HAI 1 Q= 1 2 | sebuah || c | | b | , HAI 1 F= 1 2 | b || c | | sebuah | . 17
Karena segitiga ABC terdapat pada lingkaran z ´ z = 1, maka | sebuah | = | b | = | c | = 1,→ | sebuah 2 | = | b 2 | = | c 2 | = 1 2 | sebuah || b | | c | = 1 2 | sebuah || c | | b | = 1 2 | b || c | | sebuah | = 1 2 Jadi, titik D, E, F, K, L, M, N, Q, F termasuk dalam lingkaran yang sama Teorema Gauss Jika sebuah garis memotong garis-garis yang memuat sisi BC, CA, AB dari segitiga ABC berturut-turut, di titik A 1, B 1 , C 1, maka titik tengah ruas AA 1, BB 1, СС 1 adalah segaris. Dengan menggunakan (11), kita tuliskan kondisi kolinearitas kembar tiga titik AB 1 C, CA 1 B, BC 1 A, A 1 B 1 C 1: 0,) b - a (c) a - c () c - b (a 0 ,) c - b a() b - a () a - c b(0,) a - c b() c - b () b - a c(0,) b - a (c) a - c () c - ba (1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1             b c a b (31) Jika M, N, P adalah titik tengah dari segmen AA 1, BB 1, CC 1 , maka kita harus menunjukkan bahwa 0) () () (      n mp p m p n p n m (32) Sejak), (2 1), (2 1), (2 1 1 1 1 c c p b n am       maka persamaan yang dibuktikan (31) ekuivalen dengan ini: 0))(())(())((1 1 1 1 1 1 1 1 1                b b a a c c a a c c b b c c b a a atau setelah perkalian: 0) () () () () () () () () () () (1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1                           b a c b a dengan b a c b a c a c b a dengan b a c b a c b c b a c b a c b a c a (33) Sekarang mudah untuk melihat bahwa ( 33) diperoleh dengan menjumlahkan persamaan (31). Pembuktiannya lengkap

Bab IV.

Menyelesaikan soal USE dan berbagai olimpiade dengan menggunakan metode bilangan kompleks.
Soal 1. Ujian Negara Terpadu -2012, P-4 Pada garis yang memuat median AD segitiga siku-siku ABC dengan sudut siku-siku C, diambil sebuah titik E yang jauh dari titik sudut A dan berjarak 4. Tentukan luas daerah tersebut segitiga SM jika BC=6, AC= 4. Solusi pertama. Menurut teorema Pythagoras AD=5. Maka ED=1 Misalkan titik E terletak pada sinar AD. Median AD lebih panjang dari AE, dan titik E terletak di dalam segitiga ABC (Gbr. 1). Mari kita turunkan EF yang tegak lurus dari titik E ke garis BC dan perhatikan segitiga siku-siku DEF dan DAC. Dari persamaan segitiga tersebut kita peroleh: EF = AC ∙ ED AD = 4 5 19
Oleh karena itu, S SM = 1 2 ∙ 6 ∙ 4 5 = 2.4. Misalkan sekarang titik A terletak di antara E dan D (Gbr. 2). Dalam hal ini ED=9 dan EF = AC ∙ ED AD = 36 5 . Maka S SM = 1 2 ∙ 6 ∙ 36 5 = 21,6. Jawaban: 2.4; 21.6. Menyelesaikan masalah menggunakan bilangan kompleks. Kasus I: titik E terletak pada sinar AD. Karena D titik tengah CB, maka CD=3. Dan karena CA=4, jelas AD=5, yaitu DE=1. Misalkan titik C sebagai titik awal, dan garis CA dan CB sebagai sumbu real dan imajiner. Kemudian A(4), C(0), B(6i), D(3i), E(e). Titik A, E dan D segaris, maka e − 4 3i − e = 4 yaitu e= 12i + 4 5 . Berdasarkan rumus (25) S CBE =│ ´ i 4 (e6 ´ i +6i(− ´ e)│= e e − ´ ¿ 6 i 2 4 ¿ ¿ =2.4 Kasus II: titik A terletak di antara titik D dan E , maka 4 − e 3i − 4 = 4 5 , yaitu e= 36 − 12 i 5 S CBE = | 3 i 2 2 (36 − 12 i 5 − − 36 − 12i 5) | cara pertama, Anda perlu memiliki sejumlah tebakan, yang mungkin tidak langsung muncul, tetapi setelah melalui pemikiran yang cukup lama. Padahal, jika siswa sudah mempersiapkan diri dengan baik, maka solusinya sendiri akan terbentuk secara instan cara kedua, kami menggunakan rumus yang sudah jadi, sehingga menghemat waktu dalam pencarian. Namun, kami memahami bahwa tanpa mengetahui rumusnya, masalah tidak dapat diselesaikan dengan menggunakan metode bilangan kompleks .
Tugas 2 (MIOO, 2011):
“Titik M terletak pada ruas AB. Pada lingkaran berdiameter AB diambil titik C yang berjarak masing-masing 20, 14 dan 15 dari titik A, M, dan B. Carilah luas segitiga BMC." 20
Penyelesaian: Karena AB adalah diameter lingkaran, maka ∆ ABC adalah persegi panjang, ∠ C = 90 ° Misalkan C sebagai titik nol pada bidang tersebut, maka A(20i), B(15), M(z). Karena CM=14 maka persamaan z ´ z = 196 sah, yaitu titik M ∈ lingkaran yang berpusat di titik C dan r=14. Cari titik potong lingkaran ini dengan garis AB: Persamaan garis AB (10a): 20 i (15 −´ z) + 15 (´ z + 20 i) + z (− 20 i − 15) = 0 Menggantikan ´ z dengan 196 z dan mengalikan seluruh persamaan dengan (4 i − 3) , kita memperoleh persamaan kuadrat untuk z: 25 z 2 + 120 i (4 i − 3) z + 196 (4 i − 3) 2 = 0 z 1,2 = 2 (3 − 4 i) (6 i± √ 13) 5 Dengan menggunakan rumus (28), kita mencari luas ∆ MBC: S = i 4 (z (´ b − ´ c) + b (´ c − ´ z) + c (´ z − ´ b)) Dimana c = 0, ´ c = 0, b = 15, ´ b = 15, ´ z = 196 ∗ 5 2 (3 − 4 i) (6 i ± √ 13) Setelah selesai transformasi yang setara, kita peroleh S = 54 ± 12 √ 13 persegi. unit Menjawab. 54 ± 12 √ 13 persegi. unit Jika Anda memecahkan masalah tersebut metode geometris, maka perlu mempertimbangkan dua kasus yang berbeda: 1 - titik M terletak di antara A dan D; 2 - antara D dan B. 21

Ketika menyelesaikan suatu masalah dengan menggunakan metode bilangan kompleks, dualitas penyelesaian diperoleh karena adanya dua titik potong lingkaran dan garis. Keadaan ini memungkinkan kita untuk menghindari kesalahan umum.
Masalah 3
Median AA 1, BB 1 dan CC 1 segitiga ABC berpotongan di titik M. Diketahui AB=6MC 1. Buktikan bahwa segitiga ABC adalah segitiga siku-siku. Penyelesaian: Misalkan C adalah titik nol pada bidang tersebut, dan tetapkan satuan nyata pada titik A. Masalahnya kemudian direduksi menjadi pembuktian bahwa b adalah bilangan imajiner murni. AB 2 = (b − 1) (´ b − 1) . M adalah pusat massa, koordinatnya adalah 1 3 b + 1 3 MC 1 2 = (1 3 b + 1 3 − 1 2 b − 1 2)(1 3 ´ b + 1 3 − 1 2 ´ b − 1 2) = 1 3 b (b + 1) (´ b + 1) Karena AB=6MC 1, maka (b − 1) (´ b − 1) = (b + 1) (´ b + 1) . Setelah melakukan transformasi, kita memperoleh b =− ´ b, yaitu b adalah bilangan imajiner murni, yaitu sudut C adalah garis lurus.
Tugas 4.
22
Akibat rotasi 90° di sekitar titik O, ruas AB berubah menjadi ruas A “B”. Buktikan median OM segitiga OAB " tegak lurus terhadap garis A " B . Penyelesaian: Misalkan koordinat O, A, B masing-masing sama dengan 0,1, b. Maka titik A " dan B " akan mempunyai koordinat a" = i dan b" = bi, dan titik tengah M ruas AB " akan mempunyai koordinat m = 1 2 (1 + bi). Kita cari: a " − b m − 0 = i − b 1 2 (1 + bi) = 2 i (i − b) i − b = 2i bilangan tersebut murni khayalan. Berdasarkan kriteria tegak lurus (ruas AB dan CD tegak lurus jika dan hanya jika bilangan a − b c − d murni khayal), garis OM dan A ’ B tegak lurus.
Masalah 5
. 23
Dari alas ketinggian segitiga, garis tegak lurus dijatuhkan ke dua sisi yang tidak sesuai dengan ketinggian tersebut. Buktikan bahwa jarak antara alas garis tegak lurus tersebut tidak bergantung pada pilihan tinggi segitiga. Penyelesaian: Diketahui segitiga ABC, dan lingkaran yang dibatasi di sekelilingnya mempunyai persamaan z ´ z = 1. Jika CD adalah tinggi segitiga, maka d = 1 2 (a + b + c − ab c) Koordinat kompleks alas M dan N dari garis tegak lurus yang dijatuhkan dari titik D ke AC dan BC berturut-turut adalah sama dengan m = 1 2 (a + c + d − ac ´ d 2) n = 1 2 (b + c + d − bc ´ d 2) Kita peroleh: m − n = 1 2 (a − b + c ´ d ( b − a)) = 1 2 ( a − b) (1 − c ´ d) = (a − b) (a − c) (b − c) 4 ab Karena | sebuah | = | b | = 1,lalu | m − n | = | (a − b) × (b − c) (c − a) | 4. Ungkapan ini simetris terhadap a, b, c, yaitu. jarak MN tidak bergantung pada pilihan tinggi segitiga.
Kesimpulan
24
"Tentu! Semua permasalahan dapat diselesaikan tanpa bilangan kompleks. Namun faktanya adalah aljabar bilangan kompleks adalah hal lain metode yang efektif memecahkan masalah planimetri. Kami hanya dapat berbicara tentang memilih metode yang lebih efektif untuk tugas tertentu. Perselisihan mengenai keunggulan suatu metode tertentu tidak ada gunanya jika kita mempertimbangkan metode-metode tersebut secara umum, tanpa penerapan pada masalah tertentu” [2]. Tempat penting dalam studi metode ditempati oleh seperangkat rumus. Ini
kelemahan utama
metode dan pada saat yang sama
harga diri
, karena ini memungkinkan Anda untuk menyelesaikan cukup banyak tugas yang kompleks menurut rumus yang sudah jadi dengan perhitungan dasar. Selain itu, saya percaya itu ketika menyelesaikan masalah planimetri metode ini bersifat universal.
Bibliografi
1. Markushevich A.I. Bilangan kompleks dan pemetaan konformal - M.: Rumah Penerbitan Negara literatur teknis dan teoritis, 1954. – 52 hal. 25
2. Ponarin Ya.P. Aljabar bilangan kompleks dalam masalah geometri: Buku untuk siswa kelas matematika sekolah, guru dan mahasiswa universitas pedagogi - M.: MTsNMO, 2004. - 160 hal. 3. Shvetsov D. Dari garis Simson ke teorema Droz-Farny, Kvant. - Nomor 6 Tahun 2009. – hal. 44-48 4.Yaglom I.M. Transformasi geometris. Transformasi linier dan melingkar. - Rumah Penerbitan Negara Sastra Teknis dan Teoritis, 1956. – 612 hal. 5. Yaglom I.M. Bilangan kompleks dan penerapannya dalam geometri - M.: Fizmatgiz, 1963. - 192 hal. 6. Morkovich A.G. dan lain-lain, Aljabar dan permulaan analisis matematika kelas 10. Dalam 2 jam Bagian 1. Buku teks untuk siswa lembaga pendidikan umum (tingkat profil) - M.: Mnemosyne, 2012. - 343 hal. 7. Andronov I.K. Matematika bilangan real dan kompleks - M.: Prosveshchenie, 1975. - 158 hal. 26

Aplikasi

Teorema klasik geometri dasar

teorema Newton.
Pada suatu segi empat yang dibatasi di sekitar lingkaran, titik tengah diagonal-diagonalnya segaris dengan pusat lingkaran. 27
Bukti. Mari kita ambil pusat lingkaran sebagai titik asal, atur jari-jarinya sama dengan satu. Mari kita nyatakan titik-titik kontak sisi-sisi segitiga segi empat ini A o B o C o D o dengan A, B, C, D (dalam urutan melingkar) (Gbr. 4). Misalkan M dan N berturut-turut adalah titik tengah diagonal A o C o dan B o D o. Maka menurut rumus titik potong garis singgung lingkaran z = 2ab a + b, titik A o , B o , C o , D o masing-masing mempunyai koordinat kompleks: , 2 , 2 , 2 , 2 0 0 0 0 d c cd d c b bc c ba ab b d a ad a         dimana a, b, c, d adalah koordinat kompleks titik A, B, C, D. Oleh karena itu.) (2 1 ,) (2 1 0 0 0 0 d c cd ba ab d b n c b bc da ad c a m             Hitung.))(())((a d c bd c ba n m      Sejak, 1 , 1 b b a a   , 1 , 1 d d c c   maka secara langsung jelas n m n m  Berdasarkan persamaan (6), titik O, M, N segaris.
teorema Pascal

.
Titik potong garis-garis yang memuat sisi-sisi yang berhadapan pada suatu segi enam terletak pada satu garis. 28
Bukti. Misalkan segi enam ABCDEF dan P FA CD N EF BC M DE AB   ) () (,) () (,) () (   (Gbr. 6) tertulis dalam lingkaran (Gbr. 6). Mari kita ambil pusat lingkaran sebagai titik nol pada bidang, dan jari-jarinya adalah per satuan panjang. Maka, menurut (17), kita mempunyai: ,) (,) (,) (fa cd a f d c p ef bc fe c b n de ab e dbam                Hitung) )(())((ef bc de ab ab fa ef de cd bc e b n m           dan sejenisnya .))(())((fa cd ef bc bc ab fa ef de cd f c p n           Selanjutnya kita temukan: .))(())((de ab c f fa cd e b p n n m        Karena bilangan-bilangan f e d c b a masing-masing sama, f e d c b a 1 , 1 , 1 , 1, 1, 1, maka pemeriksaan lisan mengungkapkan bahwa ekspresi yang ditemukan bertepatan dengan konjugasinya, yaitu bilangan real. Artinya titik M, N, P segaris.
teorema Monge.
Pada suatu segiempat yang berbentuk lingkaran, garis-garis yang melalui titik tengah sisi-sisinya dan. Setiap diagonal tegak lurus terhadap sisi yang berlawanan dan karenanya diagonal lainnya berpotongan di satu titik. Ini disebut titik Monge dari segi empat siklik. Bukti. Garis bagi yang tegak lurus sisi-sisi segi empat ABCD berpotongan di pusat lingkaran yang dibatasi, yang kita ambil sebagai titik pangkal. Untuk setiap titik M(z) dari garis bagi yang tegak lurus terhadap [AB] bilangan b a b a z   ) (2 1 murni khayalan. 29
Khususnya, untuk z=0 sama dengan) (2) (b a b a    . Untuk setiap titik N(z) dari garis yang melalui titik tengah sisi CD tegak lurus (AB), bilangan b a d c z   ) (2 1 harus murni imajiner dan sebaliknya. Tapi untuk z=) (2 1 d c b a    sama) (2 b a b a   yaitu murni imajiner. Oleh karena itu, titik E dengan koordinat kompleks) (2 1 d c b a    terletak pada garis yang ditunjukkan Dan persamaan ini simetris terhadap huruf a, b, c, d. Oleh karena itu, lima garis lainnya yang dikonstruksi serupa mengandung titik E. 30

• Kami akan didasarkan pada koneksi, bukan pada rumus mekanis.
• Mari kita pertimbangkan bilangan kompleks sebagai pelengkap sistem bilangan kita, sama seperti bilangan nol, pecahan, atau negatif.
• Kami memvisualisasikan ide dalam bentuk grafik untuk lebih memahami esensinya, dan tidak hanya menyajikannya dalam teks kering.

Dan milik kita senjata rahasia: belajar dengan analogi. Kita akan membahas bilangan kompleks dengan memulai dari nenek moyangnya, yaitu bilangan negatif. Berikut sedikit panduan untuk Anda:

Untuk saat ini, tabel ini tidak masuk akal, tapi biarkan saja. Di akhir artikel, semuanya akan beres.

Mari kita pahami betul apa itu bilangan negatif

Angka negatif tidak sesederhana itu. Bayangkan Anda adalah seorang ahli matematika Eropa pada abad ke-18. Anda mempunyai 3 dan 4, dan Anda dapat menulis 4 – 3 = 1. Sederhana saja.

Tapi apa itu 3 – 4? Apa sebenarnya maksudnya ini? Bagaimana Anda bisa mengambil 4 ekor sapi dari 3 ekor? Bagaimana Anda bisa mendapatkan lebih sedikit daripada tidak sama sekali?

Bilangan negatif dipandang sebagai omong kosong belaka, sesuatu yang “membayangi seluruh teori persamaan” (Francis Maceres, 1759). Saat ini, sangatlah tidak masuk akal jika menganggap angka negatif sebagai sesuatu yang tidak logis dan tidak membantu. Tanyakan kepada guru Anda apakah bilangan negatif melanggar matematika dasar.

Apa yang telah terjadi? Kami menemukan bilangan teoretis yang memiliki sifat berguna. Angka negatif tidak bisa disentuh atau dirasakan, namun bagus dalam menggambarkan hubungan tertentu (seperti utang, misalnya). Ini adalah ide yang sangat berguna.

Daripada berkata, “Aku berhutang padamu 30,” dan membaca kata-katanya untuk mengetahui apakah aku dalam keadaan hitam atau hitam, aku bisa menuliskan “-30” dan mengetahui apa maksudnya. Jika saya menghasilkan uang dan melunasi hutang saya (-30 + 100 = 70), saya dapat dengan mudah menulis transaksi ini dalam beberapa karakter. Saya akan mendapatkan +70.

Tanda plus dan minus secara otomatis menunjukkan arah - Anda tidak memerlukan satu kalimat lengkap untuk menjelaskan perubahan setelah setiap transaksi. Matematika menjadi lebih sederhana, lebih elegan. Tidak lagi menjadi masalah apakah angka negatif itu "nyata" - mereka punya fitur yang bermanfaat, dan kami menggunakannya sampai hal tersebut menjadi tertanam kuat dalam kehidupan kami sehari-hari. Jika ada teman Anda yang belum memahami esensi bilangan negatif, kini Anda akan membantunya.

Namun jangan meremehkan penderitaan manusia: angka negatif merupakan perubahan nyata dalam kesadaran. Bahkan Euler, si jenius yang menemukan bilangan e dan masih banyak lagi, tidak memahami bilangan negatif sebaik yang kita pahami saat ini. Hal ini dipandang sebagai hasil perhitungan yang "tidak berarti".

Sungguh aneh mengharapkan anak-anak dengan tenang memahami ide-ide yang pernah membingungkan bahkan para ahli matematika terbaik sekalipun.

Memasukkan Angka Imajiner

Ini cerita yang sama dengan angka imajiner. Kita bisa menyelesaikan persamaan seperti ini sepanjang hari:

Jawabannya adalah 3 dan -3. Tapi mari kita bayangkan ada orang pintar yang menambahkan nilai minus di sini:

Baiklah. Pertanyaan seperti inilah yang membuat orang merasa ngeri saat pertama kali melihatnya. Apakah Anda ingin menghitung akar kuadrat suatu bilangan yang kurang dari nol? Ini tidak terpikirkan! (Secara historis, pertanyaan serupa sebenarnya ada, tetapi akan lebih mudah bagi saya untuk membayangkan orang bijak yang tidak berwajah, agar tidak mempermalukan para ilmuwan di masa lalu).

Kelihatannya gila, sama seperti bilangan negatif, nol, dan bilangan irasional (bilangan tidak berulang) di masa lalu. Tidak ada arti "nyata" dari pertanyaan ini, bukan?

Tidak, itu tidak benar. Apa yang disebut “bilangan imajiner” sama normalnya dengan bilangan lain (atau sama abnormalnya): bilangan tersebut adalah alat untuk menggambarkan dunia. Dengan semangat yang sama ketika kita membayangkan bahwa -1, 0,3 dan 0 "ada", misalkan ada suatu bilangan i, dimana:

Dengan kata lain, Anda mengalikan i dengan dirinya sendiri untuk mendapatkan -1. Apa yang terjadi sekarang?

Yah, awalnya kita pasti pusing. Namun dengan memainkan permainan "Anggap saja saya ada" sebenarnya kita membuat matematika menjadi lebih sederhana dan elegan. Muncul koneksi-koneksi baru yang dapat kita gambarkan dengan mudah.

Anda tidak akan percaya pada i, sama seperti para ahli matematika tua yang pemarah itu tidak percaya akan keberadaan -1. Semua konsep baru yang memutar otak menjadi sebuah tabung sulit untuk dipahami, dan maknanya tidak segera muncul, bahkan bagi Euler yang brilian. Namun seperti yang ditunjukkan oleh angka negatif, ide-ide baru yang aneh bisa sangat berguna.

Saya tidak suka istilah "bilangan imajiner" itu sendiri - sepertinya istilah itu dipilih secara khusus untuk menyinggung perasaan saya. Angka i sama normalnya dengan yang lain, namun julukan “imajiner” sudah menempel di sana, jadi kami juga akan menggunakannya.

Pemahaman visual tentang bilangan negatif dan kompleks

Persamaan x^2 = 9 sebenarnya berarti sebagai berikut:

Transformasi x manakah yang diterapkan dua kali dan mengubah 1 menjadi 9?

Ada dua jawaban: "x = 3" dan "x = -3". Artinya, Anda dapat “menskalakan” sebanyak 3 kali atau “menskalakan sebanyak 3 dan membalik” (membalikkan atau mengambil kebalikan dari hasilnya adalah semua interpretasi mengalikan dengan satu negatif).

Sekarang mari kita pikirkan persamaan x^2 = -1, yang dapat ditulis seperti ini:

Transformasi x manakah yang diterapkan dua kali dan mengubah 1 menjadi -1? Hm.

• Kita tidak bisa mengalikan dua kali nomor positif karena hasilnya akan positif.
• Kita tidak bisa mengalikan bilangan negatif dua kali karena hasilnya akan positif lagi.

Bagaimana dengan... rotasi! Kedengarannya tidak biasa tentunya, tetapi bagaimana jika kita menganggap x sebagai “rotasi 90 derajat”, maka dengan menerapkan x dua kali kita akan membuat rotasi 180 derajat sebesar sumbu koordinat, dan 1 akan berubah menjadi -1!

Wow! Dan jika kita memikirkannya lebih jauh, kita dapat melakukan dua putaran dalam arah yang berlawanan, dan juga beralih dari 1 ke -1. Ini adalah rotasi "negatif" atau perkalian dengan -i:

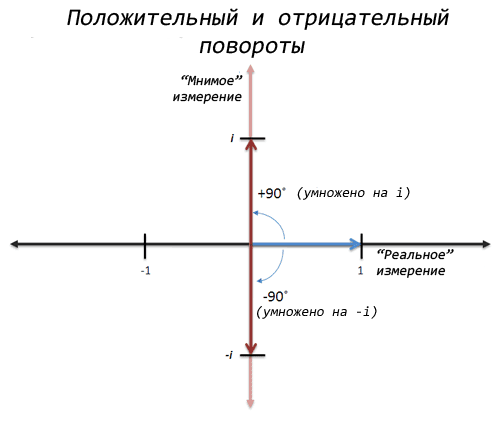
Jika kita mengalikan dengan -i dua kali, maka pada perkalian pertama kita mendapatkan -i dari 1, dan pada perkalian kedua -1 dari -i. Jadi sebenarnya ada dua akar kuadrat-1: saya dan -i.

Ini sangat keren! Kita punya solusinya, tapi apa maksudnya?

• i adalah "dimensi imajiner baru" untuk mengukur bilangan
• i (atau -i) adalah angka yang "menjadi" ketika diputar
• Mengalikannya dengan i berarti memutar 90 derajat berlawanan arah jarum jam
• Perkalian dengan -i adalah putaran 90 derajat searah jarum jam.
• Memutar dua kali ke arah mana pun menghasilkan -1: ini membawa kita kembali ke dimensi "normal" bilangan positif dan negatif (sumbu x).

Semua bilangan adalah 2 dimensi. Ya, memang sulit untuk menerimanya, namun sama sulitnya bagi orang Romawi kuno untuk menerimanya. desimal atau pembagian panjang. (Bagaimana bisa ada lebih banyak angka antara 1 dan 2?). Terlihat aneh seperti orang lain jalan baru berpikir dalam matematika.

Kami bertanya "Bagaimana cara mengubah 1 menjadi -1 dalam dua tindakan?" dan menemukan jawabannya: putar 1 90 derajat dua kali. Cara berpikir yang cukup aneh dan baru dalam matematika. Tapi sangat berguna. (Omong-omong, interpretasi geometris bilangan kompleks ini muncul hanya beberapa dekade setelah ditemukannya bilangan i itu sendiri).

Juga, jangan lupa bahwa melakukan revolusi berlawanan arah jarum jam adalah hal yang direkomendasikan hasil positif- ini murni konvensi manusia, dan semuanya bisa saja sangat berbeda.

Cari set

Mari kita bahas lebih dalam tentang detailnya. Saat Anda mengalikan bilangan negatif (seperti -1), Anda mendapatkan himpunan:

• 1, -1, 1, -1, 1, -1, 1, -1

Karena -1 tidak mengubah besar kecilnya bilangan, hanya tandanya saja, maka diperoleh bilangan yang sama baik dengan tanda “+” maupun dengan tanda “-”. Untuk bilangan x yang didapat:

• x, -x, x, -x, x, -x…

Ini adalah ide yang sangat berguna. Angka “x” dapat mewakili minggu baik dan minggu buruk. Mari kita bayangkan bahwa minggu yang baik diikuti minggu yang buruk; Ini minggu yang baik; Seperti apa minggu ke-47 ini?

X berarti ini akan menjadi minggu yang buruk. Lihat bagaimana angka negatif "mengikuti tanda" - kita cukup memasukkan (-1)^47 ke dalam kalkulator alih-alih menghitung ("Minggu 1 baik, minggu 2 buruk... minggu 3 baik..."). Hal-hal yang selalu berganti-ganti dapat dimodelkan dengan sempurna menggunakan bilangan negatif.

Oke, apa yang terjadi jika kita terus mengalikannya dengan i?

Lucu sekali, mari kita sederhanakan semuanya sedikit:

Berikut hal yang sama disajikan secara grafis:

Kami mengulangi siklus ini setiap putaran ke-4. Itu tentu saja masuk akal, bukan? Setiap anak akan memberitahu Anda bahwa 4 belokan ke kiri sama dengan tidak berbelok sama sekali. Sekarang istirahatlah dari bilangan imajiner (i, i^2) dan lihat himpunan totalnya:

• X, Y, -X, -Y, X, Y, -X, -Y…

Persisnya bagaimana angka negatif dimodelkan refleksi cermin bilangan, bilangan imajiner dapat memodelkan apa saja yang berputar antara dua dimensi “X” dan “Y”. Atau apa pun yang bersifat siklis dan melingkar - apakah ada yang Anda pikirkan?

Memahami Bilangan Kompleks

Ada satu detail lagi yang perlu dipertimbangkan: bisakah suatu bilangan bersifat “nyata” dan “imajiner”?

Jangan meragukannya. Siapa bilang kita harus berbelok tepat 90 derajat? Jika kita berdiri dengan satu kaki di dimensi “nyata” dan kaki lainnya di dimensi “imajiner”, maka akan terlihat seperti ini:

Kita berada pada tanda 45 derajat, dimana bagian real dan imajinernya sama, dan bilangannya sendiri adalah “1 + i”. Ini seperti hot dog, dengan saus tomat dan mustard - siapa bilang Anda harus memilih salah satu?

Pada dasarnya, kita dapat memilih kombinasi bagian nyata dan imajiner apa pun dan membuat semuanya menjadi segitiga. Sudut tersebut menjadi “sudut rotasi”. Bilangan kompleks adalah nama mewah untuk bilangan yang memiliki bagian nyata dan bagian imajiner. Ditulis sebagai “a + bi”, dimana:

• a - bagian nyata
• b - bagian imajiner

Tidak buruk. Tapi hanya ada satu yang tersisa pertanyaan terakhir: Seberapa “besar” suatu bilangan kompleks? Kita tidak dapat mengukur bagian nyata atau bagian imajiner secara terpisah karena kita akan kehilangan gambaran besarnya.

Mari kita mundur selangkah. Besar kecilnya bilangan negatif adalah jarak dari nol:

Ini adalah cara lain untuk menemukannya nilai mutlak. Namun bagaimana cara mengukur kedua komponen pada sudut 90 derajat untuk bilangan kompleks?

Apakah itu burung di langit... atau pesawat terbang... Pythagoras datang untuk menyelamatkan!

Teorema ini muncul jika memungkinkan, bahkan dalam angka yang ditemukan 2000 tahun setelah teorema itu sendiri. Ya, kita membuat segitiga, dan sisi miringnya sama dengan jarak dari nol:

Meskipun mengukur bilangan kompleks tidak sesederhana “menghilangkan tanda - saja”, bilangan kompleks memiliki peranan yang sangat penting aplikasi yang berguna. Mari kita lihat beberapa di antaranya.

Contoh Nyata: Rotasi

Kami tidak akan menunggu sampai perguruan tinggi fisika untuk berlatih bilangan kompleks. Kami akan melakukannya hari ini. Banyak yang bisa dikatakan tentang perkalian bilangan kompleks, tetapi untuk saat ini Anda perlu memahami hal utama:

• Perkalian dengan bilangan kompleks akan berputar berdasarkan sudutnya

Mari kita lihat cara kerjanya. Bayangkan saya berada di atas perahu, bergerak dalam lintasan 3 unit ke Timur dan 4 unit ke Utara. Saya ingin mengubah arah saya 45 derajat berlawanan arah jarum jam. Apa kursus baru saya?

Seseorang mungkin berkata, “Mudah! Hitung sinus, kosinus, cari nilai tangennya di Google... lalu..." Sepertinya kalkulatorku rusak...

Ayo pergi dengan cara yang sederhana: kita berada di jalur 3 + 4i (tidak peduli berapa sudutnya, kita tidak peduli untuk saat ini) dan kita ingin berbelok 45 derajat. Nah, 45 derajat adalah 1 + i (diagonal ideal). Jadi kita bisa mengalikan tarif kita dengan angka ini!

Inilah intinya:

• Pos awal: 3 satuan Timur, 4 satuan Utara = 3 + 4i
• Putar berlawanan arah jarum jam 45 derajat = kalikan 1 + i

Jika dikalikan kita mendapatkan:

Pedoman baru kami adalah 1 unit ke Barat (-1 ke Timur) dan 7 unit ke Utara, Anda dapat menggambar koordinat pada grafik dan mengikutinya.

Tetapi! Kami menemukan jawabannya dalam 10 detik, tanpa sinus dan cosinus. Tidak ada vektor, tidak ada matriks, tidak ada pelacakan di kuadran mana kita berada. Itu hanya perhitungan aritmatika sederhana dan sedikit aljabar. Bilangan imajiner bagus untuk rotasi!

Apalagi hasil perhitungan seperti itu sangat bermanfaat. Kita mempunyai lintasan (-1, 7) dan bukan sudut (atan(7/-1) = 98,13, dan langsung terlihat jelas bahwa kita berada di kuadran kedua. Bagaimana tepatnya Anda berencana menggambar dan mengikuti sudut yang ditunjukkan ? Menggunakan busur derajat di tangan?

Tidak, Anda akan mengubah sudut menjadi kosinus dan sinus (-0,14 dan 0,99), mencari perkiraan rasio di antara keduanya (sekitar 1 banding 7) dan membuat sketsa sebuah segitiga. Dan di sini bilangan kompleks pasti menang - akurat, secepat kilat, dan tanpa kalkulator!

Jika Anda seperti saya, Anda akan menganggap penemuan ini menakjubkan. Jika tidak, saya khawatir matematika tidak membuat Anda bersemangat sama sekali. Maaf!

Trigonometri memang bagus, tetapi bilangan kompleks membuat penghitungan lebih mudah (seperti mencari cos(a + b)). Ini hanyalah pengumuman kecil; pada artikel berikut ini saya akan memberikan menu lengkapnya.

Penyimpangan liris: beberapa orang berpikir seperti ini: “Hei, tidak nyaman jika ada arah Utara/Timur daripada sudut sederhana untuk lewatnya kapal!

Apakah itu benar? Oke, lihat milikmu tangan kanan. Berapakah sudut antara pangkal jari kelingking dan ujung jari telunjuk? Semoga berhasil dengan metode perhitungan Anda.

Atau Anda cukup menjawab, “Ujungnya X inci ke kanan dan Y inci ke atas,” dan Anda dapat melakukan sesuatu untuk mengatasinya.

Apakah bilangan kompleks semakin dekat?

Kami mempelajari penemuan dasar saya di bidang bilangan kompleks seperti tornado. Lihatlah ilustrasi pertama, sekarang seharusnya menjadi lebih jelas.

Masih banyak lagi yang bisa ditemukan dalam angka-angka indah dan menakjubkan ini, tapi otak saya sudah lelah. Tujuan saya sederhana:

• Meyakinkan Anda bahwa bilangan kompleks hanya dipandang “gila”, namun nyatanya bisa sangat berguna (seperti halnya bilangan negatif)
• Tunjukkan bagaimana bilangan kompleks dapat menyederhanakan beberapa soal seperti rotasi.

Jika saya tampak terlalu khawatir tentang topik ini, ada alasannya. Angka khayalan telah menjadi obsesi saya selama bertahun-tahun - kurangnya pemahaman membuat saya jengkel.

Namun menyalakan lilin lebih baik daripada mengarungi kegelapan pekat: inilah pemikiran saya, dan saya yakin cahaya tersebut akan menerangi benak para pembaca saya.

Epilog: Tapi mereka masih cukup aneh!

Aku tahu mereka juga masih terlihat aneh bagiku. Saya mencoba berpikir seperti orang pertama yang tidak menemukan pemikiran apa pun.

Nol adalah ide yang aneh, “sesuatu” mewakili “ketiadaan”, dan ini tidak dapat dipahami dengan cara apa pun Roma kuno. Sama halnya dengan bilangan kompleks - ini adalah cara berpikir yang baru. Namun bilangan nol dan bilangan kompleks sangat menyederhanakan matematika. Jika kita tidak pernah memperkenalkan hal-hal aneh seperti sistem bilangan baru, kita akan tetap menghitung semuanya dengan jari kita.

Saya ulangi analogi ini karena sangat mudah untuk mulai berpikir bahwa bilangan kompleks itu "tidak normal". Mari kita terbuka terhadap inovasi: di masa depan, orang hanya akan bercanda tentang bagaimana seseorang hingga abad ke-21 tidak percaya pada bilangan kompleks.