Cara mencari asimtot pada grafik suatu fungsi. Berapa banyak asimtot yang dimiliki grafik suatu fungsi? Asimtot vertikal dari grafik suatu fungsi

Bagaimana cara menyisipkan rumus matematika pada website?

Jika Anda perlu menambahkan satu atau dua rumus matematika ke halaman web, maka cara termudah untuk melakukannya adalah seperti yang dijelaskan dalam artikel: rumus matematika dengan mudah dimasukkan ke situs dalam bentuk gambar yang dibuat secara otomatis oleh Wolfram Alpha . Selain kesederhanaannya, metode universal ini akan membantu meningkatkan visibilitas situs di mesin pencari. Ini telah berfungsi sejak lama (dan, menurut saya, akan berfungsi selamanya), tetapi secara moral sudah ketinggalan zaman.

Jika Anda sering menggunakan rumus matematika di situs Anda, saya sarankan Anda menggunakan MathJax - pustaka JavaScript khusus yang menampilkan notasi matematika di browser web menggunakan markup MathML, LaTeX, atau ASCIIMathML.

Ada dua cara untuk mulai menggunakan MathJax: (1) menggunakan kode sederhana, Anda dapat dengan cepat menghubungkan skrip MathJax ke situs web Anda, yang akan secara otomatis dimuat dari server jauh pada waktu yang tepat (daftar server); (2) unduh skrip MathJax dari server jauh ke server Anda dan sambungkan ke semua halaman situs Anda. Metode kedua - lebih rumit dan memakan waktu - akan mempercepat pemuatan halaman situs Anda, dan jika server induk MathJax untuk sementara tidak tersedia karena alasan tertentu, ini tidak akan memengaruhi situs Anda dengan cara apa pun. Terlepas dari kelebihan ini, saya memilih metode pertama karena lebih sederhana, lebih cepat dan tidak memerlukan keahlian teknis. Ikuti contoh saya, dan hanya dalam 5 menit Anda akan dapat menggunakan semua fitur MathJax di situs Anda.

Anda dapat menghubungkan skrip perpustakaan MathJax dari server jauh menggunakan dua opsi kode yang diambil dari situs web utama MathJax atau di halaman dokumentasi:

Salah satu opsi kode ini perlu disalin dan ditempelkan ke dalam kode laman web Anda, sebaiknya di antara tag dan atau tepat setelah tag. Menurut opsi pertama, MathJax memuat lebih cepat dan memperlambat halaman. Namun opsi kedua secara otomatis memantau dan memuat MathJax versi terbaru. Jika Anda memasukkan kode pertama, kode tersebut perlu diperbarui secara berkala. Jika Anda memasukkan kode kedua, halaman akan dimuat lebih lambat, tetapi Anda tidak perlu terus-menerus memantau pembaruan MathJax.

Cara termudah untuk menghubungkan MathJax adalah di Blogger atau WordPress: di panel kontrol situs, tambahkan widget yang dirancang untuk memasukkan kode JavaScript pihak ketiga, salin versi pertama atau kedua dari kode unduhan yang disajikan di atas ke dalamnya, dan letakkan widget lebih dekat ke awal template (omong-omong, ini sama sekali tidak diperlukan, karena skrip MathJax dimuat secara asinkron). Itu saja. Sekarang pelajari sintaks markup MathML, LaTeX, dan ASCIIMathML, dan Anda siap memasukkan rumus matematika ke halaman web situs Anda.

Setiap fraktal dibangun menurut aturan tertentu, yang diterapkan secara konsisten dalam jumlah yang tidak terbatas. Setiap waktu tersebut disebut iterasi.

Algoritme berulang untuk membuat spons Menger cukup sederhana: kubus asli dengan sisi 1 dibagi dengan bidang yang sejajar dengan permukaannya menjadi 27 kubus yang sama besar. Satu kubus pusat dan 6 kubus yang berdekatan di sepanjang sisinya dikeluarkan darinya. Hasilnya adalah satu set yang terdiri dari sisa 20 kubus kecil. Melakukan hal yang sama dengan masing-masing kubus ini, kita mendapatkan satu set yang terdiri dari 400 kubus yang lebih kecil. Melanjutkan proses ini tanpa henti, kita mendapatkan spons Menger.

Berapa banyak asimtot yang dimiliki grafik suatu fungsi?

Bukan satu, satu, dua, tiga,... atau banyak sekali. Kita tidak akan membahas terlalu jauh tentang contohnya; mari kita ingat fungsi dasarnya. Parabola, parabola kubik, dan gelombang sinus tidak mempunyai asimtot sama sekali. Grafik fungsi logaritma eksponensial memiliki satu asimtot. Tangen busur dan kotangen busur mempunyai dua buah, dan tangen serta kotangen mempunyai banyak sekali. Tidak jarang suatu graf mempunyai asimtot horizontal dan vertikal. Hiperbola, akan selalu mencintaimu.

Apa yang dimaksud dengan mencari asimtot grafik suatu fungsi?

Ini berarti mencari tahu persamaannya, dan menggambar garis lurus jika soal memerlukannya. Prosesnya melibatkan pencarian limit suatu fungsi.

Asimtot vertikal dari grafik suatu fungsi

Asimtot vertikal suatu grafik, biasanya, terletak pada titik diskontinuitas fungsi yang tak terhingga. Sederhana saja: jika pada suatu titik fungsi tersebut mengalami diskontinuitas tak terhingga, maka garis lurus yang ditentukan oleh persamaan tersebut adalah asimtot vertikal dari grafik tersebut.

Catatan: Harap dicatat bahwa entri tersebut digunakan untuk merujuk pada dua konsep yang sangat berbeda. Apakah suatu titik tersirat atau persamaan garis bergantung pada konteksnya.

Jadi, untuk menentukan keberadaan asimtot vertikal di suatu titik, cukup dengan menunjukkan bahwa setidaknya salah satu batas satu sisinya tidak terhingga. Paling sering ini adalah titik di mana penyebut fungsinya adalah nol. Pada dasarnya, kita telah menemukan asimtot vertikal pada contoh terakhir pelajaran tentang kontinuitas suatu fungsi. Tetapi dalam beberapa kasus hanya ada satu batas satu sisi, dan jika tidak terbatas, sekali lagi - suka dan sukai asimtot vertikal. Ilustrasi paling sederhana: dan sumbu ordinat.

Dari penjelasan di atas juga terdapat fakta yang jelas: jika fungsi tersebut kontinu, maka tidak ada asimtot vertikal. Untuk beberapa alasan, sebuah parabola muncul di benak saya. Sungguh, di mana Anda bisa “menempelkan” garis lurus di sini? ...ya... Saya mengerti... Pengikut Paman Freud menjadi histeris =)

Pernyataan sebaliknya umumnya salah: misalnya, fungsi tidak terdefinisi pada seluruh garis bilangan, tetapi sama sekali tidak memiliki asimtot.

Asimtot miring dari grafik suatu fungsi

Asimtot miring (sebagai kasus khusus - horizontal) dapat ditarik jika argumen fungsi cenderung “plus tak terhingga” atau “minus tak terhingga”. Oleh karena itu, grafik suatu fungsi tidak boleh memiliki lebih dari 2 asimtot miring. Misalnya, grafik fungsi eksponensial memiliki satu asimtot horizontal di, dan grafik tangen busur di memiliki dua asimtot tersebut, dan asimtotnya berbeda.

Ini persis bagaimana tugas umum dirumuskan, dan ini melibatkan pencarian SEMUA asimtot grafik (vertikal, miring/horizontal). Meskipun, lebih tepatnya dalam mengajukan pertanyaan, kita berbicara tentang penelitian tentang keberadaan asimtot (bagaimanapun juga, mungkin tidak ada sama sekali).

Mari kita mulai dengan sesuatu yang sederhana:

Contoh 1

Solusinya dapat dengan mudah dibagi menjadi dua poin:

1) Pertama kita periksa apakah ada asimtot vertikal. Penyebutnya menjadi nol di , dan langsung terlihat jelas bahwa pada titik ini fungsi tersebut mengalami diskontinuitas tak terhingga, dan garis lurus yang ditentukan oleh persamaan tersebut merupakan asimtot vertikal dari grafik fungsi tersebut. Namun, sebelum menarik kesimpulan seperti itu, perlu dicari batasan sepihak:

Saya mengingatkan Anda tentang teknik penghitungan yang juga saya fokuskan di artikel kontinuitas suatu fungsi. Poin-poin penting. Dalam ekspresi di bawah tanda limit kita substitusikan . Tidak ada yang menarik pada pembilangnya:
.

Tapi ternyata di penyebutnya bilangan negatif yang sangat kecil:
, itu menentukan nasib batas tersebut.

Limit sebelah kiri tidak terhingga, dan pada prinsipnya sudah dimungkinkan untuk membuat keputusan tentang adanya asimtot vertikal. Tetapi batasan satu sisi diperlukan tidak hanya untuk ini - batasan tersebut MEMBANTU UNTUK MEMAHAMI BAGAIMANA letak grafik suatu fungsi dan membangunnya dengan BENAR. Oleh karena itu, kita juga harus menghitung limit tangan kanan:

Kesimpulan: limit satu sisi tidak terhingga, artinya garis lurus merupakan asimtot vertikal grafik fungsi di .

Batas pertama terbatas, yang berarti perlu “melanjutkan percakapan” dan menemukan batasan kedua:

Batasan kedua juga terbatas.

Jadi, asimtot kita adalah:

Kesimpulan: garis lurus yang ditentukan oleh persamaan tersebut merupakan asimtot horizontal dari grafik fungsi di .

Untuk mencari asimtot horizontal, Anda dapat menggunakan rumus yang disederhanakan:

Jika terdapat limit berhingga, maka garis lurus tersebut merupakan asimtot horizontal grafik fungsi di .

Sangat mudah untuk melihat bahwa pembilang dan penyebut suatu fungsi memiliki orde pertumbuhan yang sama, yang berarti bahwa batas yang diinginkan akan berhingga:

Menjawab :

Sesuai syaratnya, tidak perlu membuat gambar, namun jika penelitian fungsi sudah berjalan lancar, maka kita langsung membuat sketsa pada drafnya:

Berdasarkan ketiga limit yang ditemukan, coba cari tahu sendiri bagaimana letak grafik fungsi tersebut. Apakah ini sulit? Temukan 5-6-7-8 poin dan tandai pada gambar. Namun, grafik fungsi ini dibuat menggunakan transformasi grafik fungsi dasar, dan pembaca yang mempelajari Contoh 21 artikel di atas dengan cermat dapat dengan mudah menebak jenis kurva apa tersebut.

Contoh 2

Temukan asimtot grafik suatu fungsi

Ini adalah contoh untuk Anda pecahkan sendiri. Izinkan saya mengingatkan Anda bahwa prosesnya mudah dibagi menjadi dua titik - asimtot vertikal dan asimtot miring. Dalam solusi sampel, asimtot horizontal ditemukan menggunakan skema yang disederhanakan.

Dalam praktiknya, fungsi rasional pecahan paling sering ditemui, dan setelah berlatih hiperbola, kami akan memperumit tugas:

Contoh 3

Temukan asimtot grafik suatu fungsi

Solusi: Satu, dua dan selesai:

1) Asimtot vertikal berada pada titik diskontinuitas tak terhingga, jadi Anda perlu memeriksa apakah penyebutnya mendekati nol. Mari selesaikan persamaan kuadrat:

Diskriminannya positif, sehingga persamaan mempunyai dua akar real, dan hasil usahanya meningkat secara signifikan =)

Untuk mencari limit satu sisi lebih lanjut, akan lebih mudah untuk memfaktorkan trinomial kuadrat:
(untuk notasi ringkas, tanda “minus” dimasukkan pada tanda kurung pertama). Untuk amannya mari kita cek dengan cara membuka bracket secara mental atau draft.

Mari kita tulis ulang fungsinya dalam formulir

Mari kita cari limit satu sisi pada suatu titik:

Dan intinya:

Jadi, garis lurus merupakan asimtot vertikal dari grafik fungsi yang bersangkutan.

2) Jika dilihat dari fungsinya , maka cukup jelas bahwa limitnya akan berhingga dan kita mempunyai asimtot horizontal. Mari kita tunjukkan kehadirannya secara singkat:

Jadi, garis lurus (sumbu absis) merupakan asimtot horizontal dari grafik fungsi tersebut.

Menjawab :

Limit dan asimtot yang ditemukan memberikan banyak informasi tentang grafik fungsi. Cobalah membayangkan secara mental gambar tersebut dengan mempertimbangkan fakta-fakta berikut:

Buat sketsa versi grafik Anda pada draf Anda.

Tentu saja, batasan yang ditemukan tidak secara jelas menentukan tampilan grafik, dan Anda mungkin membuat kesalahan, tetapi latihan itu sendiri akan memberikan bantuan yang sangat berharga dalam mempelajari fungsi tersebut secara menyeluruh. Gambar yang benar ada di akhir pelajaran.

Contoh 4

Temukan asimtot grafik suatu fungsi

Contoh 5

Temukan asimtot grafik suatu fungsi

Ini adalah tugas yang harus diselesaikan secara mandiri. Kedua grafik kembali memiliki asimtot horizontal, yang langsung terdeteksi oleh ciri-ciri berikut: pada Contoh 4 orde pertumbuhan penyebutnya lebih besar dari orde pertumbuhan pembilangnya, dan pada Contoh 5 pembilang dan penyebutnya berorde sama. pertumbuhan. Dalam larutan sampel, fungsi pertama diperiksa keberadaan asimtot miring secara penuh, dan fungsi kedua - hingga batasnya.

Menurut kesan subyektif saya, asimtot horizontal jauh lebih umum dibandingkan asimtot yang “benar-benar miring”. Kasus umum yang telah lama ditunggu-tunggu:

Contoh 6

Temukan asimtot grafik suatu fungsi

Solusi: genre klasik:

1) Karena penyebutnya positif, fungsi tersebut kontinu sepanjang garis bilangan, dan tidak ada asimtot vertikal. …Apakah itu bagus? Bukan kata yang tepat - luar biasa! Poin No. 1 ditutup.

2) Mari kita periksa keberadaan asimtot miring:

Batas pertama terbatas, jadi mari kita lanjutkan. Saat menghitung batas kedua untuk menghilangkan ketidakpastian “tak terhingga dikurangi tak terhingga”, kami mereduksi ekspresi menjadi penyebut yang sama:

Batasan kedua juga terbatas, oleh karena itu, grafik fungsi yang dimaksud memiliki asimtot miring:

Kesimpulan :

Jadi, ketika grafik fungsinya sangat dekat mendekati garis lurus:

Perhatikan bahwa ia memotong asimtot miringnya di titik asal, dan titik perpotongan tersebut cukup dapat diterima - penting bahwa "semuanya normal" pada jarak tak terhingga (sebenarnya, di sinilah kita berbicara tentang asimtot).

Contoh 7

Temukan asimtot grafik suatu fungsi

Solusi: tidak ada yang istimewa untuk dikomentari, jadi saya akan membuat contoh perkiraan solusi akhir:

1) Asimtot vertikal. Mari kita telusuri maksudnya.

Garis lurus merupakan asimtot vertikal grafik di .

2) Asimtot miring:

Garis lurus merupakan asimtot miring untuk grafik di .

Menjawab :

Batas dan asimtot satu sisi yang ditemukan memungkinkan kita memprediksi dengan pasti seperti apa grafik fungsi ini. Gambar yang benar di akhir pelajaran.

Contoh 8

Temukan asimtot grafik suatu fungsi

Ini adalah contoh penyelesaian independen; untuk memudahkan penghitungan beberapa limit, Anda dapat membagi pembilang dengan penyebut suku demi suku. Sekali lagi, saat menganalisis hasil Anda, coba gambarkan grafik fungsi ini.

Jelasnya, pemilik asimtot miring “nyata” adalah grafik dari fungsi rasional pecahan yang derajat pembilangnya tertinggi satu lebih besar dari derajat penyebutnya yang tertinggi. Jika lebih besar, tidak akan ada lagi asimtot miring (misalnya, ).

Namun keajaiban lain terjadi dalam hidup:

Contoh 9

Penyelesaian: fungsi tersebut kontinu pada seluruh garis bilangan, artinya tidak ada asimtot vertikal. Tapi mungkin ada juga yang cenderung. Kami memeriksa:

Saya ingat bagaimana, di universitas, saya menemukan fungsi serupa dan tidak percaya bahwa fungsi tersebut memiliki asimtot miring. Sampai saya menghitung batas kedua:

Sebenarnya, ada dua ketidakpastian di sini: dan , tetapi dengan satu atau lain cara, Anda perlu menggunakan metode solusi, yang dibahas dalam Contoh 5-6 artikel tentang batasan peningkatan kompleksitas. Kami mengalikan dan membagi dengan ekspresi konjugasi untuk menggunakan rumus:

Menjawab :

Mungkin asimtot miring yang paling populer.

Sampai saat ini, tak terhingga telah “dipotong dengan satu kuas”, tetapi kebetulan grafik suatu fungsi mempunyai dua asimtot miring yang berbeda di dan di :

Contoh 10

Periksa grafik suatu fungsi untuk mengetahui adanya asimtot

Penyelesaian: ekspresi akarnya positif, artinya domain definisinya adalah bilangan real apa pun, dan tidak boleh ada batang vertikal.

Mari kita periksa apakah ada asimtot miring.

Jika “x” cenderung “minus tak terhingga”, maka:
(saat menjumlahkan “X” di bawah akar kuadrat, Anda harus menambahkan tanda “minus” agar tidak menghilangkan negatif penyebutnya)

Kelihatannya tidak biasa, namun ketidakpastiannya adalah “tak terhingga dikurangi tak terhingga”. Kalikan pembilang dan penyebutnya dengan ekspresi konjugasinya:

Jadi, garis lurus merupakan asimtot miring dari grafik di .

Dengan "plus infinity" semuanya menjadi lebih sepele:

Dan garis lurusnya berada di .

Menjawab :

Jika ;
, Jika .

Saya tidak dapat menolak gambar grafisnya:

Ini adalah salah satu cabang hiperbola.

Bukan hal yang aneh jika potensi keberadaan asimtot pada awalnya dibatasi oleh domain fungsinya:

Contoh 11

Periksa grafik suatu fungsi untuk mengetahui adanya asimtot

Solusi: jelas , oleh karena itu kita hanya mempertimbangkan setengah bidang kanan, yang terdapat grafik fungsinya.

1) Fungsi tersebut kontinu pada interval, artinya jika ada asimtot vertikal maka hanya dapat berupa sumbu ordinat. Mari kita pelajari perilaku fungsi di dekat titik di sebelah kanan:

Harap dicatat bahwa TIDAK ada ketidakpastian di sini (kasus seperti itu ditekankan di awal artikel Metode penyelesaian batasan).

Jadi, garis lurus (sumbu ordinat) adalah asimtot vertikal grafik fungsi di .

2) Kajian terhadap asimtot miring dapat dilakukan menurut skema lengkap, namun pada artikel L'Hopital Rules kita menemukan bahwa fungsi linier mempunyai orde pertumbuhan yang lebih tinggi daripada fungsi logaritma, oleh karena itu: (Lihat Contoh 1 dari pelajaran yang sama).

Kesimpulan: sumbu x merupakan asimtot mendatar dari grafik fungsi di .

Menjawab :

Jika ;
, Jika .

Menggambar untuk kejelasan:

Sangat menarik bahwa fungsi yang tampaknya serupa tidak memiliki asimtot sama sekali (mereka yang ingin dapat memeriksanya).

Dua contoh terakhir untuk belajar mandiri:

Contoh 12

Periksa grafik suatu fungsi untuk mengetahui adanya asimtot

Untuk memeriksa asimtot vertikal, pertama-tama Anda perlu mencari domain definisi fungsi, lalu menghitung sepasang limit satu sisi pada titik yang “mencurigakan”. Asimtot miring juga tidak dikecualikan, karena fungsinya didefinisikan pada “plus” dan “minus” tak terhingga.

Contoh 13

Periksa grafik suatu fungsi untuk mengetahui adanya asimtot

Tapi di sini hanya ada asimtot miring, dan arahnya harus dipertimbangkan secara terpisah.

Saya harap Anda menemukan asimtot yang tepat =)

Aku harap kamu berhasil!

Solusi dan jawaban:

Contoh 2:Larutan :
. Mari kita cari limit satu sisi:

Lurus adalah asimtot vertikal dari grafik fungsi di .
2) Asimtot miring.

Lurus .
Menjawab :

Menggambarke Contoh 3:

Contoh 4:Larutan :
1) Asimtot vertikal. Fungsi tersebut mengalami jeda tak terhingga pada suatu titik . Mari kita hitung batas satu sisi:

Catatan: bilangan negatif yang sangat kecil hingga pangkat genap sama dengan bilangan positif yang sangat kecil: .

Lurus adalah asimtot vertikal dari grafik fungsi.
2) Asimtot miring.

Lurus (sumbu absis) adalah asimtot mendatar dari grafik fungsi di .
Menjawab :

Asimtot grafik suatu fungsi

Hantu asimtot telah lama berkeliaran di situs hingga akhirnya terwujud dalam artikel terpisah dan memberikan kegembiraan khusus bagi pembaca yang bingung dengan studi lengkap tentang fungsinya. Menemukan asimtot suatu graf adalah salah satu dari sedikit bagian tugas yang ditentukan, yang dibahas dalam kursus sekolah hanya secara ikhtisar, karena kejadiannya berkisar pada penghitungan limit fungsi, dan masih berkaitan dengan matematika yang lebih tinggi. Bagi pengunjung yang kurang memahami analisis matematis, saya rasa petunjuknya sudah jelas ;-) ...berhenti, berhenti, mau kemana? Batasan itu mudah!

Contoh asimtot langsung ditemui pada pelajaran pertama tentang grafik fungsi dasar, dan sekarang topik tersebut mendapat pembahasan rinci.

Jadi apa itu asimtot?

Membayangkan titik variabel, yang “bergerak” sepanjang grafik fungsi. Asimtot adalah garis lurus yang menuju ke sana dekat tanpa batas waktu grafik suatu fungsi mendekat ketika titik variabelnya bergerak hingga tak terhingga.

Catatan : Definisinya bermakna, jika memerlukan rumusan dalam notasi kalkulus, silakan merujuk ke buku teks.

Di pesawat, asimtot diklasifikasikan menurut lokasi aslinya:

1) Asimtot vertikal, yang diberikan oleh persamaan bentuk, dimana “alpha” adalah bilangan real. Perwakilan populer mendefinisikan sumbu ordinat itu sendiri,
dengan sedikit rasa mual kita teringat hiperbola.

2) Asimtot miring secara tradisional ditulis dengan persamaan garis lurus dengan koefisien sudut. Terkadang kasus khusus diidentifikasi sebagai kelompok terpisah - asimtot horizontal. Misalnya hiperbola yang sama dengan asimtot.

Ayo cepat, mari kita mulai topik dengan ledakan singkat tembakan senapan mesin:

Berapa banyak asimtot yang dimiliki grafik suatu fungsi?

Apa artinya?

Asimtot vertikal dari grafik suatu fungsi

Catatan Asimtot vertikal suatu grafik, biasanya, terletak pada titik diskontinuitas fungsi yang tak terhingga. Sederhana saja: jika pada suatu titik fungsi tersebut mengalami diskontinuitas tak terhingga, maka garis lurus yang ditentukan oleh persamaan tersebut adalah asimtot vertikal dari grafik tersebut.

: Perhatikan bahwa entri tersebut digunakan untuk merujuk pada dua konsep yang sangat berbeda. Apakah suatu titik tersirat atau persamaan garis bergantung pada konteksnya. tak terbatas. Paling sering ini adalah titik di mana penyebut fungsinya adalah nol. Pada dasarnya, kita telah menemukan asimtot vertikal pada contoh terakhir pelajaran tentang kontinuitas suatu fungsi. Namun dalam beberapa kasus hanya ada satu batas satu sisi, dan jika tidak terbatas, sekali lagi - cintai dan sukai asimtot vertikal. Ilustrasi paling sederhana: dan sumbu ordinat (lihat Grafik dan properti fungsi dasar).

Dari penjelasan di atas juga terdapat fakta yang jelas: jika fungsinya kontinu pada , maka tidak ada asimtot vertikal. Untuk beberapa alasan, sebuah parabola muncul di benak saya. Sungguh, di mana Anda bisa “menempelkan” garis lurus di sini? ...ya... Saya mengerti... Pengikut Paman Freud menjadi histeris =)

Pernyataan sebaliknya umumnya salah: misalnya, fungsi tidak terdefinisi pada seluruh garis bilangan, tetapi sama sekali tidak memiliki asimtot.

Asimtot miring dari grafik suatu fungsi

Asimtot miring (sebagai kasus khusus - horizontal) dapat ditarik jika argumen fungsi cenderung “plus tak terhingga” atau “minus tak terhingga”. Oleh karena itu, grafik suatu fungsi tidak boleh memiliki lebih dari dua asimtot miring. Misalnya, grafik fungsi eksponensial memiliki satu asimtot horizontal di , dan grafik tangen busur di memiliki dua asimtot tersebut, dan asimtotnya berbeda.

Ketika grafik di kedua tempat mendekati asimtot miring tunggal, maka “tak terhingga” biasanya digabungkan dalam satu entri. Misalnya, ... Anda menebak dengan benar: .

Aturan umum:

Jika ada dua terakhir membatasi , maka garis lurus tersebut merupakan asimtot miring dari grafik fungsi di . Jika setidaknya salah satu dari batas yang tercantum tidak terbatas, maka tidak ada asimtot miring.

Catatan : rumus tetap valid jika “x” hanya cenderung ke “plus infinity” atau hanya ke “minus infinity”.

Mari kita tunjukkan bahwa parabola tidak mempunyai asimtot miring:

Limitnya tidak terhingga, artinya tidak ada asimtot miring. Perhatikan bahwa dalam mencari limit kebutuhan telah hilang sejak jawabannya telah diterima.

Catatan : Jika anda (atau akan mengalami) kesulitan memahami tanda plus-minus, minus-plus, silakan lihat bantuan di awal pelajaran
tentang fungsi yang sangat kecil, di mana saya berbicara tentang cara menafsirkan tanda-tanda ini dengan benar.

Jelas, setiap fungsi kuadrat, kubik, polinomial derajat ke-4 dan lebih tinggi juga tidak memiliki asimtot miring.

Sekarang mari kita pastikan bahwa grafik tersebut juga tidak memiliki asimtot miring. Untuk mengungkap ketidakpastian, kami menggunakan aturan L'Hopital:
, itulah yang perlu diperiksa.

Namun, jika fungsi tersebut bertambah tanpa batas, tidak ada garis lurus yang dapat didekati grafiknya sangat dekat.

Mari kita beralih ke bagian praktis dari pelajaran ini:

Bagaimana cara mencari asimtot grafik suatu fungsi?

Contoh 1

Temukan asimtot grafik suatu fungsi

Solusinya dapat dengan mudah dibagi menjadi dua poin:

Saya mengingatkan Anda tentang teknik penghitungan yang juga saya fokuskan di artikel Kontinuitas suatu fungsi. Poin-poin penting. Dalam ekspresi di bawah tanda limit kita substitusikan . Tidak ada yang menarik pada pembilangnya:
.

Tapi ternyata di penyebutnya bilangan negatif yang sangat kecil:
, itu menentukan nasib batas tersebut.

Kesimpulan: limit satu sisi tidak terhingga, artinya garis lurus merupakan asimtot vertikal grafik fungsi di .

Batas pertama terbatas, yang berarti perlu “melanjutkan percakapan” dan menemukan batasan kedua:

Batasan kedua juga terbatas.

Jadi, asimtot kita adalah:

Kesimpulan: garis lurus yang ditentukan oleh persamaan tersebut merupakan asimtot horizontal dari grafik fungsi di .

Untuk mencari asimtot horizontal
Anda dapat menggunakan rumus yang disederhanakan:

Jika ada terbatas limit, maka garis lurus tersebut merupakan asimtot mendatar dari grafik fungsi di .

Sangat mudah untuk melihat bahwa pembilang dan penyebut suatu fungsi memiliki orde pertumbuhan yang sama, yang berarti bahwa batas yang diinginkan akan berhingga:

Menjawab :

Contoh 2

Temukan asimtot grafik suatu fungsi

Ini adalah contoh untuk Anda pecahkan sendiri. Izinkan saya mengingatkan Anda bahwa prosesnya mudah dibagi menjadi dua titik – asimtot vertikal dan asimtot miring. Dalam solusi sampel, asimtot horizontal ditemukan menggunakan skema yang disederhanakan.

Dalam praktiknya, fungsi rasional pecahan paling sering ditemui, dan setelah berlatih hiperbola, kami akan memperumit tugas:

Contoh 3

Temukan asimtot grafik suatu fungsi

Solusi: Satu, dua dan selesai:

Mari kita tulis ulang fungsinya dalam formulir

Mari kita cari limit satu sisi pada suatu titik:

Dan intinya:

Jadi, garis lurus merupakan asimtot vertikal dari grafik fungsi yang bersangkutan.

2) Jika dilihat dari fungsinya , maka cukup jelas bahwa limitnya akan berhingga dan kita mempunyai asimtot horizontal. Mari kita tunjukkan kehadirannya secara singkat:

Jadi, garis lurus (sumbu absis) merupakan asimtot horizontal dari grafik fungsi tersebut.

Menjawab :

Limit dan asimtot yang ditemukan memberikan banyak informasi tentang grafik fungsi. Cobalah membayangkan secara mental gambar tersebut dengan mempertimbangkan fakta-fakta berikut:

Buat sketsa versi grafik Anda pada draf Anda.

Contoh 4

Temukan asimtot grafik suatu fungsi

Contoh 5

Temukan asimtot grafik suatu fungsi

Ini adalah tugas yang harus diselesaikan secara mandiri. Kedua grafik kembali memiliki asimtot horizontal, yang langsung terdeteksi oleh ciri-ciri berikut: pada Contoh 4, urutan pertumbuhan penyebut lagi, daripada orde pertumbuhan pembilangnya, dan pada Contoh 5 pembilang dan penyebutnya memiliki orde pertumbuhan yang sama. Dalam larutan sampel, fungsi pertama diperiksa keberadaan asimtot miring secara penuh, dan fungsi kedua – hingga batasnya.

Menurut kesan subyektif saya, asimtot horizontal jauh lebih umum dibandingkan asimtot yang “benar-benar miring”. Kasus umum yang telah lama ditunggu-tunggu:

Contoh 6

Temukan asimtot grafik suatu fungsi

Solusi: genre klasik:

1) Karena penyebutnya positif, fungsi tersebut kontinu sepanjang garis bilangan, dan tidak ada asimtot vertikal. …Apakah itu bagus? Bukan kata yang tepat - luar biasa! Poin No. 1 ditutup.

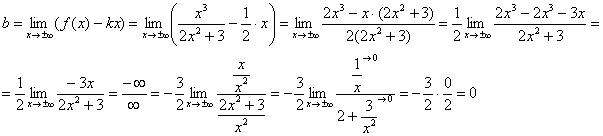
Batasan kedua juga terbatas, oleh karena itu, grafik fungsi yang dimaksud memiliki asimtot miring:

Kesimpulan :

Jadi, ketika grafik fungsinya sangat dekat mendekati garis lurus:

Contoh 7

Temukan asimtot grafik suatu fungsi

Solusi: tidak ada yang istimewa untuk dikomentari, jadi saya akan membuat contoh perkiraan solusi akhir:

1) Asimtot vertikal. Mari kita telusuri maksudnya.

Garis lurus merupakan asimtot vertikal grafik di .

2) Asimtot miring:

Garis lurus merupakan asimtot miring untuk grafik di .

Menjawab :

Batas dan asimtot satu sisi yang ditemukan memungkinkan kita memprediksi dengan pasti seperti apa grafik fungsi ini. Gambar yang benar di akhir pelajaran.

Contoh 8

Temukan asimtot grafik suatu fungsi

Namun keajaiban lain terjadi dalam hidup:

Contoh 9

Contoh 11

Periksa grafik suatu fungsi untuk mengetahui adanya asimtot

Solusi: jelas , oleh karena itu kita hanya mempertimbangkan setengah bidang kanan, yang terdapat grafik fungsinya.

Jadi, garis lurus (sumbu ordinat) adalah asimtot vertikal grafik fungsi di .

2) Kajian terhadap asimtot miring dapat dilakukan sesuai skema lengkap, namun pada artikel Aturan L'Hôpital kita menemukan bahwa fungsi linier mempunyai orde pertumbuhan yang lebih tinggi daripada fungsi logaritma, oleh karena itu: (Lihat Contoh 1 dari pelajaran yang sama).

Kesimpulan: sumbu x merupakan asimtot mendatar dari grafik fungsi di .

Menjawab :
, Jika ;
, Jika .

Menggambar untuk kejelasan:

Sangat menarik bahwa fungsi yang tampaknya serupa tidak memiliki asimtot sama sekali (mereka yang ingin dapat memeriksanya).

Dua contoh terakhir untuk belajar mandiri:

Contoh 12

Periksa grafik suatu fungsi untuk mengetahui adanya asimtot

Asimtot grafik fungsi y = f(x) adalah garis lurus yang mempunyai sifat jarak dari titik (x, f(x)) ke garis lurus tersebut cenderung nol karena titik grafik bergerak tak terhingga dari asal.

Pada Gambar 3.10. contoh grafis asimtot vertikal, horizontal dan miring diberikan.

Pencarian asimtot grafik didasarkan pada tiga teorema berikut.

Teorema asimtot vertikal. Biarkan fungsi y = f(x) terdefinisi di lingkungan tertentu dari titik x 0 (mungkin tidak termasuk titik itu sendiri) dan setidaknya salah satu batas satu sisi dari fungsi tersebut sama dengan tak terhingga, yaitu. Maka garis lurus x = x 0 merupakan asimtot vertikal dari grafik fungsi y = f(x).

Jelasnya, garis lurus x = x 0 tidak dapat menjadi asimtot vertikal jika fungsinya kontinu di titik x 0, karena dalam hal ini . Akibatnya, asimtot vertikal harus dicari pada titik diskontinuitas fungsi atau pada ujung domain definisinya.

Teorema asimtot horizontal. Misalkan fungsi y = f(x) terdefinisi untuk x yang cukup besar dan terdapat limit fungsi yang berhingga. Maka garis y = b merupakan asimtot mendatar dari grafik fungsi tersebut.

Komentar. Jika hanya salah satu limitnya yang berhingga, maka fungsi tersebut masing-masing mempunyai asimtot horizontal sisi kiri atau sisi kanan.

Jika , fungsi tersebut mungkin memiliki asimtot miring.

Teorema asimtot miring. Misalkan fungsi y = f(x) terdefinisi untuk x yang cukup besar dan terdapat limit yang berhingga . Maka garis lurus y = kx + b merupakan asimtot miring dari grafik fungsi tersebut.

Tidak ada bukti.

Asimtot miring, seperti halnya asimtot horizontal, dapat berupa asimtot kanan atau kiri jika alas batas yang bersesuaian mengandung tak terhingga dari suatu tanda tertentu.

Mempelajari fungsi dan membuat grafiknya biasanya mencakup langkah-langkah berikut:

1. Temukan domain definisi fungsi.

2. Periksa fungsi paritas genap-ganjil.

3. Temukan asimtot vertikal dengan memeriksa titik diskontinuitas dan perilaku fungsi pada batas domain definisi, jika terbatas.

4. Temukan asimtot horizontal atau miring dengan memeriksa perilaku fungsi di tak terhingga.

5. Temukan ekstrem dan interval monotonisitas fungsi tersebut.

6. Tentukan interval konveksitas fungsi dan titik belok.

7. Temukan titik potong dengan sumbu koordinat dan, mungkin, beberapa titik tambahan yang memperjelas grafik.

Diferensial fungsi

Dapat dibuktikan bahwa jika suatu fungsi mempunyai limit yang sama dengan suatu bilangan berhingga untuk suatu basis tertentu, maka fungsi tersebut dapat direpresentasikan sebagai jumlah dari bilangan tersebut dan nilai yang sangat kecil untuk basis yang sama (dan sebaliknya): .

Mari kita terapkan teorema ini pada fungsi terdiferensiasi: .

Jadi, kenaikan fungsi Dу terdiri dari dua suku: 1) linier terhadap Dx, yaitu. f `(x)Dх; 2) nonlinier terhadap Dx, yaitu. a(Dx)Dx. Pada saat yang sama, sejak itu , suku kedua ini sangat kecil dari orde yang lebih tinggi daripada Dx (karena Dx cenderung nol, ia cenderung lebih cepat ke nol).

Diferensial suatu fungsi adalah bagian utama, linier relatif terhadap Dx dari kenaikan fungsi, sama dengan produk turunannya dan kenaikan variabel bebas dy = f `(x)Dx.

Mari kita cari diferensial dari fungsi y = x.

Karena dy = f `(x)Dх = x`Dх = Dх, maka dx = Dх, yaitu. diferensial suatu variabel bebas sama dengan kenaikan variabel tersebut.

Oleh karena itu, rumus diferensial suatu fungsi dapat ditulis sebagai dy = f `(x)dх. Oleh karena itu, salah satu notasi turunannya adalah pecahan dy/dх.

Arti geometris dari diferensial diilustrasikan
Gambar 3.11. Mari kita ambil titik sembarang M(x, y) pada grafik fungsi y = f(x). Mari kita berikan argumen x kenaikan Dx. Maka fungsi y = f(x) akan menerima kenaikan Dy = f(x + Dx) - f(x). Mari kita menggambar garis singgung grafik fungsi di titik M, yang membentuk sudut a dengan arah positif sumbu absis, yaitu. f `(x) = tan a. Dari segitiga siku-siku MKN
KN = MN*tg a = Dх*tg a = f `(x)Dх = dy.

Jadi, diferensial suatu fungsi adalah pertambahan ordinat garis singgung yang ditarik ke grafik fungsi pada suatu titik tertentu ketika x menerima pertambahan Dx.

Sifat-sifat diferensial pada dasarnya sama dengan sifat-sifat turunan:

3. d(u ± v) = du ± dv.

4. d(uv) = v du + kamu dv.

5. d(kamu/v) = (v du - kamu dv)/v 2.

Namun, ada sifat penting dari diferensial suatu fungsi yang tidak dimiliki turunannya - yaitu invarian bentuk diferensial.

Dari definisi diferensial fungsi y = f(x), maka diferensial dy = f `(x)dх. Jika fungsi y ini kompleks, mis. y = f(u), dimana u = j(x), maka y = f dan f `(x) = f `(u)*u`. Maka dy = f `(u)*u`dх. Tapi untuk fungsinya
u = j(x) diferensial du = u`dх. Oleh karena itu dy = f `(u)*du.

Membandingkan persamaan dy = f `(x)dх dan dy = f `(u)*du, kita pastikan bahwa rumus diferensial tidak berubah jika alih-alih fungsi dari variabel bebas x kita mempertimbangkan fungsi dari variabel terikat kamu. Sifat diferensial ini disebut invarian (yaitu, kekekalan) dari bentuk (atau rumus) diferensial.

Namun, masih terdapat perbedaan dalam kedua rumus ini: pada rumus pertama, selisih variabel bebas sama dengan kenaikan variabel tersebut, yaitu. dx = Dx, dan kedua, diferensial fungsi du hanyalah bagian linier dari kenaikan fungsi Du dan hanya untuk Dx kecil du » Du.

KGB dan UFO - informasi yang dideklasifikasi dokumen rahasia KGB dan UFO

Persamaan garis dalam ruang adalah persamaan dua bidang yang berpotongan