Satu set operasi yang memungkinkan fungsi tertentu f(t) temukan karakteristik spektral yang sesuai F( sayaω) disebut Transformasi Fourier:
Secara simbolis kita akan menuliskan rumus (1) dalam bentuk
Integral di ruas kanan (1), seperti sebelumnya, dipahami dalam pengertian nilai pokok, yaitu.
Kesetaraan (1) menjalin hubungan antar fungsi f(t), argumen siapa T, dan fungsi kompleks terkaitnya F( sayaω), memiliki frekuensi ω sebagai argumen.
Rumus integral Fourier
memungkinkan dari fungsi yang diketahui F( sayaω) tentukan fungsi yang sesuai f(t). Atas dasar ini rumus (3) disebut transformasi Fourier terbalik. Kami akan menulis secara simbolis
Dalam sejumlah tugas kontrol otomatis, fungsinya f(t) mencirikan suatu proses yang berlangsung hanya dimulai dari titik waktu tertentu T, yang dapat dianggap nol.
Pada kasus ini f(t) ≡ 0 jam T< 0 (1) принимает вид
Transformasi (5) disebut transformasi Fourier satu arah langsung.Transformasi Fourier terbalik, yang berhubungan dengan transformasi satu sisi langsung, tetap dua sisi dalam variabel ω dan diberikan oleh persamaan
Pada t= 0, nilai ruas kanan (6) adalah 
;
pada T < 0 , f(t) ≡ 0
Hubungan antara Fourier dan Laplace mengubah Formula
Transformasi Laplace langsung dapat dianggap sebagai hasil generalisasi transformasi Fourier satu sisi yang dibangun dengan cara tertentu.
Misalkan, f(t) memenuhi kondisi Dirichlet pada interval 0 ≤ T< ∞ , dan f(t) ≡ 0 jam T< 0.
Seperti diketahui, transformasi Fourier dapat diterapkan pada fungsi f(t), yang integralnya 
ada (kondisi keterpaduan mutlak). Kondisi ini tidak dipenuhi oleh banyak fungsi yang digunakan dalam analisis proses pada sistem otomatis, misalnya 1( T), Asin(ω T), Acos(ω t), e pada
untuk α >0, T dan sebagainya.
Agar dapat memiliki fungsi seperti itu f(t) ditransformasikan dengan Fourier, terlebih dahulu harus dikalikan dengan e -ct dimana bilangan real C>C 0 dipilih sehingga integral 
akan konvergen.
Nilai C 0 untuk setiap fungsi f(t) cukup pasti. Dengan menggunakan rumus transformasi Fourier satu arah langsung, kita akan mentransformasikan menurut Fourier bukan f(t) , A f(t)e -ct, memenuhi kondisi untuk menerapkan transformasi ini.
Memperkenalkan variabel kompleks baru S=c+jω, kita peroleh 
.
Ungkapan ini adalah rumus transformasi Laplace langsung. Jadi, transformasi Laplace merupakan hasil perluasan transformasi Fourier ke fungsi yang memenuhi kondisi Direchlet pada interval 0 Jika F(jω) adalah spektral x – tick f(t), maka fungsi F(S) dari variabel kompleks S adalah karakteristik spektral dari fungsi waktu peluruhan f(t)e -ct. Perhatikan rumus transformasi Fourier terbalik: Gantikan f(t) di sisi kanan dan kiri persamaan ini dengan f(t)e -ct , kita peroleh: Mengingat S=e + jω, dω=dS/j, kita temukan Persamaan ini merupakan rumus transformasi Laplace invers, yaitu. transformasi invers Laplace dapat dianggap sebagai pengembangan dari transformasi Fourier invers. Telah disebutkan sebelumnya bahwa representasi suatu fungsi dalam bentuk integral Fourier sesuai dengan representasi suatu fungsi sebagai jumlah harmonik yang jumlahnya tak terhingga dengan amplitudo yang sangat kecil, dan frekuensi harmonik berbeda dari satu sama lain sangat kecil. Demikian pula dengan representasi ini, f(t) dalam bentuk (*) sesuai dengan representasi fungsi ini dalam bentuk komponen yang sangat kecil dalam jumlah tak terhingga, yang merupakan osilasi dengan amplitudo yang sangat kecil, meluruh menurut hukum eksponensial. Sifat-sifat transformasi Fourier mirip dengan sifat-sifat transformasi Laplace. Karakteristik spektral dari beberapa fungsi 1. Fungsi satuan langkah. Delta adalah sebuah fungsi. Fungsi 1(t) dari formulir disebut fungsi satuan langkah. Dari (1) dapat disimpulkan bahwa 1(t) pada t=0 mempunyai diskontinuitas ketidakpastian jenis pertama, dan nilai fungsi pada titik diskontinuitas tidak terdefinisi. Namun, 1(t) pada t=0 diberikan nilai yang cukup spesifik. Fungsi yang paling umum adalah sebagai berikut: Pilihan satu atau beberapa nilai fungsi satuan t=0 berkaitan dengan karakteristik masalah yang dipecahkan. Misalnya, representasi pertama berguna jika fungsi 1(t) dianggap sebagai limit sebagai λ→∞ dari barisan fungsi kontinu: f(t,λ)=1/2+(1/π)arctg λt (3) , dimana λ adalah parameter dan Urutan fungsi kontinu karena λ→ ∞ juga memiliki representasi pertama 1(t) sebagai limitnya. Untuk memeriksa apakah program bekerja dengan benar, kita akan membentuk array sampel sebagai jumlah dari dua sinusoida sin(10*2*pi*x)+0.5*sin(5*2*pi*x) dan memasukkannya ke dalam program . Program ini menggambarkan hal-hal berikut: Gambar 1 Grafik fungsi waktu sinyal Pada grafik spektrum terdapat dua batang (harmonik) 5 Hz dengan amplitudo 0,5 V dan 10 Hz dengan amplitudo 1 V, semuanya sama seperti pada rumus sinyal aslinya. Semuanya baik-baik saja, programmer yang hebat! Program ini bekerja dengan benar. Artinya jika kita menerapkan sinyal nyata dari campuran dua sinusoida ke input ADC, kita akan mendapatkan spektrum serupa yang terdiri dari dua harmonik. Total, milik kita nyata sinyal terukur berlangsung 5 detik, didigitalkan oleh ADC, yaitu diwakili terpisah penting, punya diskrit non-periodik jangkauan. Sepertinya ada yang tidak beres! Harmonik 10 Hz digambar secara normal, tetapi alih-alih tongkat 5 Hz, muncul beberapa harmonik aneh. Kami mencari di Internet untuk melihat apa yang terjadi... Ya, mereka mengatakan bahwa Anda perlu menambahkan angka nol di akhir sampel dan spektrum akan digambarkan seperti biasa. Itu masih tidak sama seperti pada 5 detik. Kita harus berurusan dengan teorinya. Mari pergi ke Wikipedia- sumber pengetahuan. K - bilangan fungsi trigonometri (bilangan komponen harmonik, bilangan harmonik) Apa yang dimaksud dengan “mewakili suatu fungsi sebagai jumlah suatu deret”? Artinya dengan menjumlahkan nilai komponen harmonik deret Fourier di setiap titik, kita memperoleh nilai fungsi kita di titik tersebut. (Lebih tepatnya, deviasi akar-rata-rata-kuadrat suatu deret dari fungsi f(x) akan cenderung ke nol, namun meskipun terdapat konvergensi akar-rata-rata-kuadrat, deret Fourier suatu fungsi, secara umum, tidak diperlukan untuk konvergen ke sana secara langsung. Lihat https://ru.wikipedia.org/wiki/Fourier_Series.) Seri ini juga dapat ditulis sebagai: Hubungan antara koefisien (1) dan (3) dinyatakan dengan rumus berikut: Perhatikan bahwa ketiga representasi deret Fourier ini sepenuhnya setara. Terkadang, saat bekerja dengan deret Fourier, lebih mudah menggunakan eksponen argumen imajiner daripada sinus dan cosinus, yaitu menggunakan transformasi Fourier dalam bentuk kompleks. Tetapi akan lebih mudah bagi kita untuk menggunakan rumus (1), di mana deret Fourier direpresentasikan sebagai jumlah kosinus dengan amplitudo dan fase yang sesuai. Bagaimanapun, adalah salah untuk mengatakan bahwa transformasi Fourier dari sinyal nyata akan menghasilkan amplitudo harmonik yang kompleks. Seperti yang dinyatakan dengan benar oleh Wiki, “Transformasi Fourier (ℱ) adalah operasi yang mengaitkan satu fungsi dari variabel nyata dengan fungsi lain, juga variabel nyata.” Total: Transformasi Fourier memungkinkan Anda untuk merepresentasikan fungsi kontinu f(x) (sinyal), yang didefinisikan pada segmen (0, T) sebagai jumlah dari bilangan tak hingga (deret tak hingga) dari fungsi trigonometri (sinus dan/atau kosinus) dengan tertentu amplitudo dan fase, juga dipertimbangkan pada segmen (0, T). Deret seperti ini disebut deret Fourier. Mari kita perhatikan beberapa poin lagi, yang pemahamannya diperlukan untuk penerapan transformasi Fourier yang benar pada analisis sinyal. Jika kita perhatikan deret Fourier (jumlah sinusoidal) pada seluruh sumbu X, kita dapat melihat bahwa di luar segmen (0, T) fungsi yang diwakili oleh deret Fourier akan mengulangi fungsi kita secara berkala. Misalnya, pada grafik Gambar 7, fungsi asli didefinisikan pada segmen (-T\2, +T\2), dan deret Fourier mewakili fungsi periodik yang didefinisikan pada seluruh sumbu x. Hal ini terjadi karena sinusoidal itu sendiri merupakan fungsi periodik, sehingga jumlahnya akan menjadi fungsi periodik. Dengan demikian: Fungsi awal kita kontinu, non-periodik, terdefinisi pada segmen tertentu dengan panjang T. Periode komponen harmonik adalah kelipatan nilai segmen (0, T) yang fungsi aslinya f(x) terdefinisi. Dengan kata lain, periode harmonik merupakan kelipatan durasi pengukuran sinyal. Misalnya, periode harmonik pertama deret Fourier sama dengan interval T di mana fungsi f(x) terdefinisi. Periode harmonik kedua deret Fourier sama dengan interval T/2. Dan seterusnya (lihat Gambar 8). Oleh karena itu, frekuensi komponen harmonik adalah kelipatan 1/T. Artinya, frekuensi komponen harmonik Fk sama dengan Fk= k\T, dengan k berkisar antara 0 hingga ∞, misalnya k=0 F0=0; k=1 F1=1\T; k=2 F2=2\T; k=3 F3=3\T;… Fk= k\T (pada frekuensi nol - komponen konstan). Biarkan fungsi awal kita menjadi sinyal yang direkam selama T=1 detik. Maka periode harmonik pertama akan sama dengan durasi sinyal kita T1=T=1 detik dan frekuensi harmoniknya adalah 1 Hz. Periode harmonik kedua akan sama dengan durasi sinyal dibagi 2 (T2=T/2=0,5 detik) dan frekuensinya adalah 2 Hz. Untuk harmonik ketiga T3=T/3 detik dan frekuensinya 3 Hz. Dan seterusnya. Langkah antar harmonisa dalam hal ini adalah 1 Hz. Dengan demikian, suatu sinyal yang berdurasi 1 detik dapat diuraikan menjadi komponen harmonik (memperoleh spektrum) dengan resolusi frekuensi 1 Hz. Ada cara untuk meningkatkan durasi sinyal secara artifisial dengan menambahkan angka nol ke array sampel. Tapi itu tidak meningkatkan resolusi frekuensi sebenarnya. Skema biasa untuk mengukur dan mendigitalkan sinyal adalah sebagai berikut. Sinyal dari transduser pengukur tiba di ADC selama periode waktu T. Sampel sinyal (sampling) yang diperoleh selama waktu T dikirimkan ke komputer dan disimpan dalam memori. Apa persyaratan untuk parameter digitalisasi sinyal? Perangkat yang mengubah sinyal input analog menjadi kode diskrit (sinyal digital) disebut konverter analog-ke-digital (ADC) (Wiki). Salah satu parameter utama ADC adalah frekuensi pengambilan sampel maksimum (atau laju pengambilan sampel, laju sampel bahasa Inggris) - laju pengambilan sampel dari sinyal kontinu waktu saat pengambilan sampelnya. Itu diukur dalam Hertz. ((Wiki)) Menurut teorema Kotelnikov, jika sinyal kontinu mempunyai spektrum yang dibatasi oleh frekuensi Fmax, maka sinyal tersebut dapat direkonstruksi secara lengkap dan unik dari sampel diskritnya yang diambil pada interval waktu. Apa yang akan terjadi jika kita mengambil sampel dengan frekuensi lebih rendah dari yang disyaratkan oleh teorema Kotelnikov? Dalam hal ini, terjadi efek “aliasing” (juga dikenal sebagai efek stroboskopik, efek moire), di mana sinyal frekuensi tinggi, setelah digitalisasi, berubah menjadi sinyal frekuensi rendah, yang sebenarnya tidak ada. Pada Gambar. 11 gelombang sinus frekuensi tinggi merah adalah sinyal nyata. Sinusoid biru dengan frekuensi lebih rendah adalah sinyal fiktif yang muncul karena fakta bahwa selama waktu pengambilan sampel lebih dari setengah periode sinyal frekuensi tinggi berhasil dilewati. Untuk menghindari efek aliasing, filter anti-aliasing khusus ditempatkan di depan ADC - filter low-pass (LPF), yang melewatkan frekuensi di bawah setengah frekuensi sampling ADC, dan memotong frekuensi yang lebih tinggi. Untuk menghitung spektrum sinyal dari sampel diskritnya, digunakan transformasi Fourier diskrit (DFT). Mari kita perhatikan sekali lagi bahwa spektrum sinyal diskrit “menurut definisi” dibatasi oleh frekuensi Fmax, yang kurang dari setengah frekuensi sampling Fd. Oleh karena itu, spektrum sinyal diskrit dapat diwakili oleh jumlah sejumlah harmonik yang terbatas, berbeda dengan jumlah tak terbatas untuk deret Fourier dari sinyal kontinu, yang spektrumnya tidak terbatas. Menurut teorema Kotelnikov, frekuensi maksimum suatu harmonik harus sedemikian rupa sehingga mencakup setidaknya dua sampel, sehingga jumlah harmonik sama dengan setengah jumlah sampel sinyal diskrit. Artinya, jika terdapat N sampel dalam suatu sampel, maka jumlah harmonisa pada spektrumnya akan sama dengan N/2. Sekarang mari kita perhatikan transformasi Fourier diskrit (DFT). Bandingkan dengan deret Fourier Kita melihat bahwa keduanya bertepatan, kecuali waktu dalam DFT bersifat diskrit dan jumlah harmonik dibatasi oleh N/2 - setengah dari jumlah sampel. Rumus DFT ditulis dalam variabel bilangan bulat tak berdimensi k, s, dimana k adalah jumlah sampel sinyal, s adalah jumlah komponen spektral. Kembali ke hasil yang diperoleh di awal. Seperti disebutkan di atas, ketika fungsi non-periodik (sinyal kita) diperluas menjadi deret Fourier, deret Fourier yang dihasilkan sebenarnya sesuai dengan fungsi periodik dengan periode T (Gbr. 12). Seperti terlihat pada Gambar 12, fungsi f(x) periodik dengan periode T0. Namun karena durasi sampel pengukuran T tidak bertepatan dengan periode fungsi T0, maka fungsi yang diperoleh sebagai deret Fourier memiliki diskontinuitas di titik T. Akibatnya, spektrum fungsi ini akan mengandung sejumlah besar harmonik frekuensi tinggi. Jika durasi sampel pengukuran T bertepatan dengan periode fungsi T0, maka spektrum yang diperoleh setelah transformasi Fourier hanya akan memuat harmonik pertama (sinusoida dengan periode yang sama dengan durasi pengambilan sampel), karena fungsinya f(x) adalah sinusoida. Dengan kata lain, program DFT “tidak mengetahui” bahwa sinyal kita adalah “sepotong sinusoidal”, tetapi mencoba merepresentasikan fungsi periodik dalam bentuk rangkaian, yang memiliki diskontinuitas karena ketidakkonsistenan masing-masing bagian dari sinyal tersebut. sinusoida. Akibatnya, harmonik muncul dalam spektrum, yang seharusnya merangkum bentuk fungsinya, termasuk diskontinuitasnya. Jadi, untuk mendapatkan spektrum sinyal yang “benar”, yang merupakan jumlah dari beberapa sinusoidal dengan periode berbeda, bilangan bulat periode setiap sinusoidal harus dimasukkan ke dalam periode pengukuran sinyal. Dalam prakteknya, kondisi ini dapat dipenuhi untuk durasi pengukuran sinyal yang cukup lama. Dengan durasi yang lebih pendek, gambar akan terlihat “lebih buruk”: Dalam praktiknya, mungkin sulit untuk memahami di mana letak “komponen sebenarnya” dan di mana “artefak” yang disebabkan oleh periode non-multiple dari komponen dan durasi pengambilan sampel sinyal atau “lompatan dan jeda” dalam bentuk sinyal. . Tentu saja, kata “komponen nyata” dan “artefak” diberi tanda kutip karena suatu alasan. Kehadiran banyak harmonisa pada grafik spektrum tidak berarti bahwa sinyal kita benar-benar “terdiri” dari harmonisa tersebut. Ini sama dengan berpikir bahwa angka 7 “terdiri dari” angka 3 dan 4. Angka 7 dapat direpresentasikan sebagai jumlah dari angka 3 dan 4 - ini benar. Jadi sinyal kita... atau lebih tepatnya bukan “sinyal kita”, tetapi fungsi periodik yang disusun dengan mengulangi sinyal kita (sampling) dapat direpresentasikan sebagai jumlah harmonik (gelombang sinus) dengan amplitudo dan fase tertentu. Namun dalam banyak kasus yang penting untuk praktik (lihat gambar di atas), harmonik yang diperoleh dalam spektrum memang dapat dikaitkan dengan proses nyata yang bersifat siklik dan memberikan kontribusi signifikan terhadap bentuk sinyal. 2. Sinyal diwakili oleh sekumpulan nilai nyata dan spektrumnya diwakili oleh sekumpulan nilai nyata. Frekuensi harmonik positif. Fakta bahwa lebih mudah bagi ahli matematika untuk merepresentasikan spektrum dalam bentuk kompleks menggunakan frekuensi negatif tidak berarti bahwa “ini benar” dan “ini harus selalu dilakukan.” 3. Sinyal yang diukur dalam interval waktu T ditentukan hanya dalam interval waktu T. Apa yang terjadi sebelum kita mulai mengukur sinyal, dan apa yang akan terjadi setelah itu, tidak diketahui sains. Dan dalam kasus kami, ini tidak menarik. DFT dari sinyal berbatas waktu memberikan spektrum yang “sebenarnya”, dalam artian, dalam kondisi tertentu, memungkinkan seseorang menghitung amplitudo dan frekuensi komponen-komponennya. Bahan yang digunakan dan bahan bermanfaat lainnya. Mari kita perhatikan sifat dasar transformasi Fourier. Linearitas. Mari kita lihat fungsi dan Maka spektrum kombinasi liniernya adalah: Penundaan waktu. Kami berasumsi bahwa spektrumnya diketahui Mari kita hitung spektrum sinyal yang mengalami pergeseran waktu: Kami mendapat sinyal tertunda untuk sementara waktu Mengubah skala. Kami berasumsi bahwa spektrumnya diketahui Mengalikan dengan Jadi, mengalikan sinyal dengan Spektrum turunan. Dalam hal ini, poin kuncinya adalah keterintegrasian absolut dari fungsi tersebut. Dari kenyataan bahwa integral modulus suatu fungsi harus dibatasi, maka pada tak terhingga fungsi tersebut harus cenderung nol. Integral turunan suatu fungsi diambil sebagian, suku-suku non-integral yang dihasilkan sama dengan nol, karena fungsinya cenderung nol pada tak terhingga. Spektrum integral. Mari kita cari spektrum sinyalnya Teorema konvolusi. Diketahui bahwa Transformasi Fourier dari konvolusi dua sinyal menghasilkan produk spektrum sinyal-sinyal ini. Menghasilkan sinyal. Diketahui bahwa Spektrum produk sinyal adalah konvolusi spektrum sinyal-sinyal ini. Perhatian khusus harus diberikan pada sinyal diskrit, karena sinyal inilah yang digunakan dalam pemrosesan digital. Sinyal diskrit, tidak seperti sinyal kontinu, adalah urutan angka yang sesuai dengan nilai sinyal kontinu pada titik waktu tertentu. Secara konvensional, sinyal diskrit dapat dianggap sebagai sinyal kontinu, yang pada waktu-waktu tertentu mengambil nilai-nilai tertentu dan sama dengan nol pada waktu-waktu lainnya. Jadi, misalnya, diskrit Beras. 1. Pengambilan sampel sinyal. Pulsa berbentuk persegi panjang mempunyai durasi Amplitudo pulsa dipilih sehingga integral pulsa selama periode tersebut sama dengan Untuk mendapatkan sampel sinyal instan Perluasan fungsi deret Fourier mempunyai bentuk yang persis sama: Koefisien ekspansi ke dalam deret trigonometri sinyal pewaktuan Maka sinyal diskritnya akan terlihat seperti: Saat menghitung transformasi Fourier dari sinyal diskrit, kami menukar operasi penjumlahan dan integrasi, dan kemudian menggunakan properti δ
-fungsi: Spektrum sinyal diskrit adalah fungsi periodik. Mari kita pertimbangkan eksponen dalam suku terpisah Mari kita tampilkan yang lain Mari kita hitung Jadi, konvolusi (30) Dari persamaan (32) dapat disimpulkan bahwa spektrum sinyal diskrit adalah fungsi yang berulang secara periodik Fakta bahwa perubahan kualitatif terjadi pada spektrum sinyal sebagai hasil pengambilan sampel menunjukkan bahwa sinyal asli dapat terdistorsi, karena sinyal tersebut sepenuhnya ditentukan oleh spektrumnya. Namun, di sisi lain, pengulangan periodik dari spektrum yang sama dengan sendirinya tidak membawa sesuatu yang baru ke dalam spektrum, oleh karena itu, dalam kondisi tertentu, dengan mengetahui nilai sinyal pada titik waktu tertentu, seseorang dapat menemukan nilainya. sinyal ini diambil pada titik waktu lain, yaitu memperoleh sinyal kontinu asli. Inilah maksud dari teorema Kotelnikov yang memberikan syarat pada pemilihan frekuensi kuantisasi sesuai dengan frekuensi maksimum dalam spektrum sinyal. Jika kondisi ini dilanggar, maka setelah sinyal didigitalkan, spektrum yang berulang secara berkala akan ditumpangkan (Gbr. 2). Spektrum yang dihasilkan akan sesuai dengan sinyal yang berbeda. Beras. 2. Spektral tumpang tindih. Transformasi Fourier adalah sekumpulan metode matematika yang didasarkan pada penguraian fungsi kontinu waktu asli menjadi sekumpulan fungsi harmonik dasar (yang merupakan fungsi sinusoidal) dengan berbagai frekuensi, amplitudo, dan fase. Dari definisi tersebut jelas bahwa gagasan utama transformasi adalah bahwa fungsi apa pun dapat direpresentasikan sebagai jumlah sinusoida yang tak terhingga, yang masing-masing akan dicirikan oleh amplitudo, frekuensi, dan fase awalnya. Transformasi Fourier adalah pendiri analisis spektral. Analisis spektral adalah metode pemrosesan sinyal yang memungkinkan Anda mengkarakterisasi komposisi frekuensi sinyal yang diukur. Bergantung pada bagaimana sinyal direpresentasikan, transformasi Fourier yang berbeda digunakan. Ada beberapa jenis transformasi Fourier: – Transformasi Fourier Berkelanjutan (dalam literatur Inggris, Transformasi Fourier Waktu Lanjut – CTFT atau, singkatnya, F.T.); – Transformasi Fourier Diskrit (dalam literatur Inggris Transformasi Fourier Diskrit – DFT); – Transformasi Fast Fourier (dalam literatur Inggris Transformasi Fast Fourier – FFT). Transformasi Fourier berkelanjutan Transformasi Fourier adalah alat matematika yang digunakan dalam berbagai bidang ilmu pengetahuan. Dalam beberapa kasus, ini dapat digunakan sebagai sarana untuk memecahkan persamaan kompleks yang menggambarkan proses dinamis yang timbul di bawah pengaruh energi listrik, panas atau cahaya. Dalam kasus lain, ini memungkinkan seseorang untuk mengisolasi komponen reguler dalam sinyal getaran kompleks, yang memungkinkan interpretasi pengamatan eksperimental dalam astronomi, kedokteran, dan kimia dengan benar. Transformasi kontinu sebenarnya merupakan generalisasi deret Fourier, asalkan periode fungsi diperluas cenderung tak terhingga. Jadi, transformasi Fourier klasik berkaitan dengan spektrum sinyal yang diambil alih seluruh rentang keberadaan variabel. Ada beberapa jenis pencatatan transformasi Fourier kontinu, yang berbeda satu sama lain dalam nilai koefisien di depan integral (dua bentuk pencatatan): dimana dan merupakan transformasi Fourier suatu fungsi atau spektrum frekuensi suatu fungsi; Perlu dicatat bahwa berbagai jenis pencatatan ditemukan di berbagai bidang ilmu pengetahuan dan teknologi. Faktor normalisasi diperlukan untuk penskalaan sinyal yang benar dari domain frekuensi ke domain waktu. Faktor normalisasi mengurangi amplitudo sinyal pada keluaran konversi terbalik sehingga sesuai dengan amplitudo sinyal aslinya. Dalam literatur matematika, transformasi Fourier langsung dan terbalik dikalikan dengan faktor, sedangkan dalam fisika sering kali transformasi langsung tidak menyertakan faktor, tetapi transformasi terbalik menggunakan faktor. Jika Anda secara berurutan menghitung transformasi Fourier langsung dari sinyal tertentu, dan kemudian mengambil transformasi Fourier invers, maka hasil transformasi invers harus benar-benar sesuai dengan sinyal aslinya. Jika fungsinya ganjil pada interval (−∞, +∞), maka transformasi Fourier dapat direpresentasikan melalui fungsi sinus: Jika fungsinya genap pada interval (−∞, +∞), maka transformasi Fourier dapat direpresentasikan melalui fungsi kosinus: Jadi, transformasi Fourier kontinu memungkinkan kita untuk merepresentasikan fungsi non-periodik sebagai integral dari fungsi yang mewakili koefisien deret Fourier untuk fungsi non-periodik di setiap titik. Transformasi Fourier dapat dibalik, yaitu jika transformasi Fouriernya dihitung dari suatu fungsi, maka fungsi aslinya dapat dipulihkan secara unik dari transformasi Fourier. Yang kami maksud dengan transformasi Fourier terbalik adalah bentuk integral (dua bentuk notasi): dimana transformasi Fourier suatu fungsi atau spektrum frekuensi suatu fungsi; Jika fungsinya ganjil pada interval (−∞, +∞), maka invers transformasi Fourier dapat direpresentasikan melalui fungsi sinus: Jika fungsinya genap pada interval (−∞, +∞), maka invers transformasi Fourier dapat direpresentasikan melalui fungsi kosinus: Sebagai contoh, perhatikan fungsi berikut Karena fungsi tersebut merupakan fungsi genap, maka transformasi Fourier kontinu akan didefinisikan sebagai berikut: Hasilnya, kami memperoleh ketergantungan perubahan fungsi eksponensial yang diteliti pada interval frekuensi (lihat di bawah). Transformasi Fourier kontinu biasanya digunakan dalam teori ketika mempertimbangkan sinyal yang berubah sesuai dengan fungsi yang diberikan, tetapi dalam praktiknya biasanya digunakan untuk hasil pengukuran yang mewakili data diskrit. Hasil pengukuran dicatat secara berkala dengan frekuensi sampling tertentu, misalnya 16000 Hz atau 22000 Hz. Namun, dalam kasus umum, pembacaan diskrit bisa jadi tidak merata, tetapi hal ini mempersulit peralatan analisis matematika, dan oleh karena itu biasanya tidak digunakan dalam praktik. Ada teorema penting Kotelnikov (dalam literatur asing disebut "teorema Nyquist-Shannon", "teorema sampling"), yang menyatakan bahwa sinyal periodik analog memiliki spektrum terbatas (lebar terbatas) (0...fmax ) dapat dipulihkan secara unik tanpa distorsi dan kehilangan pada sampel diskritnya yang diambil dengan frekuensi lebih besar atau sama dengan dua kali frekuensi atas spektrum - frekuensi pengambilan sampel (fsample >= 2*fmax). Dengan kata lain, pada sampling rate 1000 Hz, sinyal dengan frekuensi hingga 500 Hz dapat direkonstruksi dari sinyal periodik analog. Perlu dicatat bahwa diskritisasi suatu fungsi berdasarkan waktu menyebabkan periodisasi spektrumnya, dan diskritisasi spektrum berdasarkan frekuensi menyebabkan periodisasi fungsi. Ini adalah salah satu transformasi Fourier yang banyak digunakan dalam algoritma pemrosesan sinyal digital. Transformasi Fourier diskrit langsung mengaitkan fungsi waktu, yang ditentukan oleh N titik pengukuran pada interval waktu tertentu, dengan fungsi lain, yang ditentukan pada interval frekuensi. Perlu diperhatikan bahwa fungsi pada domain waktu ditentukan menggunakan N-sampel, dan fungsi pada domain frekuensi ditentukan menggunakan spektrum K-fold. k ˗ indeks frekuensi. Frekuensi sinyal ke-k ditentukan oleh ekspresi dimana T adalah jangka waktu pengambilan data masukan. Transformasi diskrit langsung dapat ditulis ulang dalam komponen nyata dan imajiner. Komponen real adalah array yang berisi nilai-nilai komponen cosinus, dan komponen imajiner adalah array yang berisi nilai-nilai komponen sinus. Jelas dari ekspresi terakhir bahwa transformasi menguraikan sinyal menjadi komponen sinusoidal (yang disebut harmonik) dengan frekuensi dari satu osilasi per periode hingga N osilasi per periode. Transformasi Fourier diskrit memiliki ciri khusus, karena barisan diskrit dapat diperoleh dengan menjumlahkan fungsi dengan komposisi sinyal harmonik yang berbeda. Dengan kata lain, suatu barisan diskrit didekomposisi menjadi variabel-variabel harmonis – ambigu. Oleh karena itu, ketika fungsi diskrit diperluas menggunakan transformasi Fourier diskrit, komponen frekuensi tinggi muncul di paruh kedua spektrum yang tidak ada dalam sinyal aslinya. Spektrum frekuensi tinggi ini merupakan bayangan cermin dari bagian pertama spektrum (dalam hal frekuensi, fase dan amplitudo). Biasanya, paruh kedua spektrum tidak dipertimbangkan, dan amplitudo sinyal dari bagian pertama spektrum digandakan. Perlu dicatat bahwa penguraian fungsi kontinu tidak menyebabkan munculnya efek cermin, karena fungsi kontinu secara unik didekomposisi menjadi variabel harmonik. Amplitudo komponen DC adalah nilai rata-rata fungsi selama periode waktu yang dipilih dan ditentukan sebagai berikut: Amplitudo dan fase komponen frekuensi sinyal ditentukan oleh hubungan berikut: Nilai amplitudo dan fasa yang dihasilkan disebut notasi kutub. Vektor sinyal yang dihasilkan akan ditentukan sebagai berikut: Mari kita pertimbangkan algoritma untuk mentransformasikan fungsi tertentu secara diskrit pada interval tertentu (pada periode tertentu) dengan jumlah titik awal D berkilau Transformasi Fourier Sebagai hasil transformasi, kita memperoleh nilai nyata dan imajiner dari fungsi tersebut, yang ditentukan pada rentang frekuensi. Transformasi Fourier diskrit terbalik mengaitkan fungsi frekuensi, yang ditentukan oleh spektrum lipatan K pada interval frekuensi, dengan fungsi lain, yang ditentukan pada interval waktu. N ˗ jumlah nilai sinyal yang diukur selama suatu periode, serta multiplisitas spektrum frekuensi; k ˗ indeks frekuensi. Seperti yang telah disebutkan, transformasi Fourier diskrit mengasosiasikan N-titik sinyal diskrit dengan sampel spektral sinyal N-kompleks. Untuk menghitung satu sampel spektral, diperlukan N operasi perkalian dan penjumlahan kompleks. Dengan demikian, kompleksitas komputasi algoritma transformasi Fourier diskrit adalah kuadrat, dengan kata lain diperlukan operasi perkalian dan penjumlahan yang kompleks. Setelah mempelajari cara menghitung kepadatan spektral sinyal pulsa yang cukup sederhana namun sering ditemui, mari kita beralih ke studi sistematis tentang sifat-sifat transformasi Fourier. Sifat terpenting ini dirumuskan sebagai berikut: jika terdapat sekumpulan sinyal tertentu, maka jumlah bobot sinyal tersebut ditransformasikan Fourier sebagai berikut: Berikut adalah koefisien numerik arbitrer. Untuk membuktikan rumus (2.26), jumlah sinyal harus disubstitusikan ke dalam transformasi Fourier (2.16). Biarlah menjadi sinyal yang mengambil nilai nyata. Kepadatan spektralnya secara umum rumit: Kami mengganti ekspresi ini ke dalam rumus transformasi Fourier terbalik (2.18): Agar sinyal yang diperoleh dari transformasi ganda tersebut tetap nyata, diperlukan hal tersebut Hal ini hanya mungkin terjadi jika bagian nyata dari kerapatan spektral sinyal genap, dan bagian imajinernya merupakan fungsi frekuensi ganjil: Mari kita asumsikan bahwa korespondensi diketahui untuk sinyal tersebut. Mari kita pertimbangkan sinyal yang sama, tetapi terjadi beberapa detik kemudian. Dengan menganggap titik ini sebagai asal usul waktu yang baru, kami menyatakan sinyal yang dipindahkan ini sebagai Mari kita tunjukkan hal itu Buktinya sangat sederhana. Benar-benar, Modulus bilangan kompleks sama dengan satu untuk nilai apa pun, oleh karena itu amplitudo komponen harmonik dasar yang membentuk sinyal tidak bergantung pada posisinya pada sumbu waktu. Informasi tentang karakteristik sinyal ini terkandung dalam ketergantungan frekuensi argumen kerapatan spektralnya (spektrum fase). Mari kita asumsikan bahwa sinyal asli dapat mengalami perubahan skala waktu. Artinya peran waktu t dimainkan oleh variabel bebas baru (k adalah suatu bilangan real). Jika ini terjadi, sinyal asli “dikompresi”; jika sinyal "diregangkan" pada waktunya. Ternyata kalau begitu Benar-benar, dari situlah rumus (2.29) mengikuti. Jadi, misalnya, untuk mengompresi sinyal dalam waktu sambil mempertahankan bentuknya, komponen spektral yang sama perlu didistribusikan pada rentang frekuensi yang lebih luas dengan penurunan amplitudonya secara proporsional. Masalah berikut ini berkaitan erat dengan masalah yang dibahas di sini. Mengingat pulsa yang berbeda dari nol pada suatu segmen dan dicirikan oleh kerapatan spektral, maka diperlukan kerapatan spektral dari sinyal “pembalik waktu”, yang merupakan “salinan cermin” dari osilasi pulsa asli. Karena sudah jelas itu Setelah melakukan perubahan variabel, kami menemukannya Biarkan sinyal s(t) dan kerapatan spektralnya diberikan. Kami akan mempelajari sinyal baru dan menetapkan tujuan untuk menemukan kerapatan spektralnya - . A-priori, Transformasi Fourier adalah operasi linier, yang berarti persamaan (2.31) juga berlaku sehubungan dengan kepadatan spektral. Dengan mempertimbangkan (2.28), kita peroleh Mewakili fungsi eksponensial dengan deret Taylor: mensubstitusi deret ini ke (2.32) dan membatasi diri pada dua suku pertama, kita temukan Dengan diferensiasi, laju perubahan sinyal meningkat seiring waktu. Akibatnya modulus spektrum turunannya mempunyai nilai yang lebih besar pada daerah frekuensi tinggi dibandingkan dengan modulus spektrum sinyal aslinya. Rumus (2.33) digeneralisasikan untuk kasus spektrum turunan orde. Mudah untuk membuktikan bahwa jika , maka Jadi, membedakan suatu sinyal terhadap waktu sama dengan operasi aljabar sederhana yang mengalikan kerapatan spektral dengan suatu faktor. Oleh karena itu, biasanya dikatakan bahwa bilangan imajiner adalah operator diferensiasi yang beroperasi dalam domain frekuensi. Fungsi yang dipertimbangkan adalah antiturunan (integral tak tentu) terhadap fungsi tersebut. Dari (2.33) secara formal dapat disimpulkan bahwa spektrum antiturunan tersebut Dengan demikian, pengali berfungsi sebagai operator integrasi dalam domain frekuensi. Banyak perangkat teknik radio menggunakan apa yang disebut integrator - sistem fisik yang sinyal keluarannya sebanding dengan integral aksi masukan. Mari kita secara khusus mempertimbangkan integrator yang mengubah sinyal masukan menjadi sinyal keluaran menurut hukum berikut: Ini adalah parameter tetap. Integral tertentu yang termasuk dalam (2.36) jelas sama dengan selisih antara dua nilai antiturunan sinyal, yang satu dihitung dengan argumen t, dan yang lainnya dengan argumen . Dengan menggunakan hubungan (2.28) dan (2.35), kita memperoleh rumus hubungan antara kerapatan spektral sinyal pada input dan output: Faktor dalam tanda kurung dibatasi pada frekuensi berapa pun, sedangkan besaran penyebutnya bertambah secara linier seiring bertambahnya frekuensi. Hal ini menunjukkan bahwa integrator tersebut bertindak seperti filter low-pass, melemahkan komponen spektral frekuensi tinggi dari sinyal input.
Gambar.2 Grafik spektrum sinyalDari sudut pandang matematis, berapa banyak kesalahan yang terdapat dalam frasa ini?
Sekarang pihak berwenang sudah memutuskan, kami memutuskan 5 detik terlalu lama, mari kita ukur sinyalnya dalam 0,5 detik. 
Gbr.3 Grafik fungsi sin(10*2*pi*x)+0,5*sin(5*2*pi*x) untuk periode pengukuran 0,5 detik
Gambar.4 Spektrum fungsi
Gbr.5 Menambahkan angka nol hingga 5 detik
Gbr.6 Spektrum yang diterima2. Fungsi kontinu dan representasi deret Fouriernya
Secara matematis, sinyal kita dengan durasi T detik adalah fungsi tertentu f(x) yang ditentukan pada interval (0, T) (X dalam hal ini adalah waktu). Fungsi seperti itu selalu dapat direpresentasikan sebagai jumlah fungsi harmonik (sinus atau kosinus) dalam bentuk: 
(1), dimana:
T - segmen di mana fungsinya ditentukan (durasi sinyal)
Ak adalah amplitudo komponen harmonik ke-k,
θk- fase awal komponen harmonik ke-k
(2),
dimana , amplitudo kompleks ke-k.
Dasar matematis untuk analisis spektral sinyal adalah transformasi Fourier.
Gbr.7 Representasi fungsi asli non-periodik dengan deret Fourier
Spektrum fungsi ini bersifat diskrit, yaitu disajikan dalam bentuk rangkaian komponen harmonik tak terhingga - deret Fourier.
Faktanya, deret Fourier mendefinisikan fungsi periodik tertentu yang bertepatan dengan fungsi kita pada segmen (0, T), tetapi bagi kami periodisitas ini tidak signifikan.
Gbr.8 Periode (frekuensi) komponen harmonik deret Fourier (di sini T = 2π)
Untuk meningkatkan resolusi sebanyak 2 kali menjadi 0,5 Hz, Anda perlu meningkatkan durasi pengukuran sebanyak 2 kali - hingga 2 detik. Sinyal yang berdurasi 10 detik dapat diuraikan menjadi komponen harmonik (untuk memperoleh spektrum) dengan resolusi frekuensi 0,1 Hz. Tidak ada cara lain untuk meningkatkan resolusi frekuensi.3. Sinyal diskrit dan transformasi Fourier diskrit
Dengan berkembangnya teknologi digital, cara penyimpanan data pengukuran (sinyal) juga mengalami perubahan. Jika sebelumnya sinyal dapat direkam pada tape recorder dan disimpan pada tape dalam bentuk analog, kini sinyal didigitalkan dan disimpan dalam file di memori komputer sebagai sekumpulan angka (sampel). 
Gambar.9 Diagram saluran pengukuran
Gambar 10 Sinyal digital - N sampel diterima selama waktu T
, yaitu. dengan frekuensi Fd ≥ 2*Fmax, dimana Fd adalah frekuensi sampling; Fmax - frekuensi maksimum spektrum sinyal. Dengan kata lain frekuensi digitalisasi sinyal (frekuensi sampling ADC) minimal harus 2 kali lebih tinggi dari frekuensi maksimum sinyal yang ingin kita ukur.
Beras. 11. Munculnya sinyal frekuensi rendah palsu pada frekuensi pengambilan sampel yang tidak cukup tinggi
Nilai s menunjukkan jumlah osilasi harmonik lengkap selama periode T (durasi pengukuran sinyal). Transformasi Fourier diskrit digunakan untuk mencari amplitudo dan fase harmonik dengan menggunakan metode numerik, yaitu. "di komputer"
Gambar 12 Fungsi periodik f(x) dengan periode T0, dengan periode pengukuran T>T0
Gambar 13 Contoh fungsi dan spektrum sinyal kesalahan kinematik gearbox
Gambar 14 Contoh fungsi dan spektrum sinyal getaran rotorBeberapa hasil
1. Sinyal terukur nyata dengan durasi T detik, didigitalkan oleh ADC, yaitu diwakili oleh sekumpulan sampel diskrit (N buah), memiliki spektrum non-periodik diskrit, diwakili oleh sekumpulan harmonik (N/ 2 buah). 
, memiliki spektrum 
Dan 
:
(12)
sinyal 
(14)
. Mari kita nyatakan argumen fungsi sebagai variabel baru 
, Kemudian 
Dan 
menyebabkan spektrum dikalikan 
.
sinyal 
seperti melalui 
spektrum sinyal dinyatakan 
. Perkenalkan variabel baru 
, kami mengubah variabel integrasi 
.
(16)
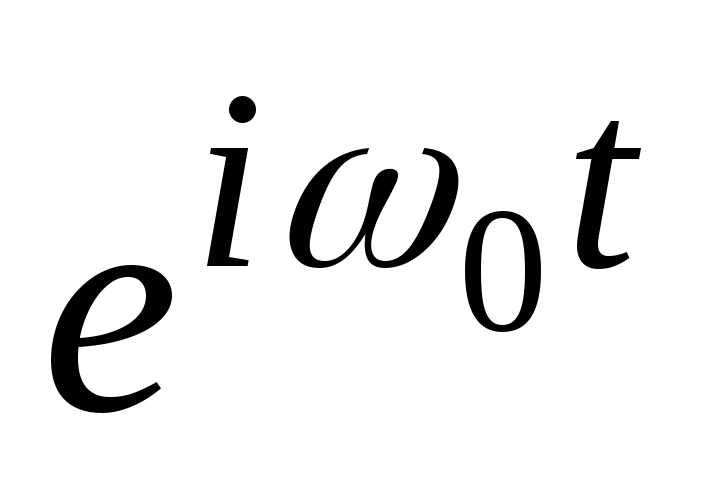. Seperti pada kasus sebelumnya, kita berasumsi bahwa spektrumnya diketahui 
sinyal 
. Mari kita cari spektrum sinyal ini dikalikan
.
menyebabkan pergeseran spektrum sebesar 
.
(18)
. Selain itu, kami akan berasumsi demikian 
, yaitu sinyal tidak memiliki komponen konstan. Persyaratan ini diperlukan agar suku-suku non-integral sama dengan nol ketika integral diambil sebagian.
(19)
Dan 
spektrum fungsi 
Dan 
masing-masing. Diperlukan untuk menyatakan spektrum konvolusi 
melalui 
Dan 
. Untuk melakukan ini, dalam integral Fourier dari konvolusi salah satu fungsi, kita menggantinya dengan variabel 
, maka substitusi dapat dilakukan dalam eksponen 
. Akibat penggantian ini, integral rangkap akan sama dengan hasil kali dua integral Fourier.
(20)
Dan 
– spektrum fungsi 
Dan 
masing-masing. Diperlukan untuk menyatakan spektrum produk 
melalui spektrum 
Dan 
. Mari kita substitusikan ke integral Fourier sebagai ganti salah satu sinyal, misalnya 
, ekspresinya melalui transformasi Fourier terbalik, dan kemudian kita mengubah urutan integrasi.
(21)Spektrum sinyal diskrit
sinyal dapat ditentukan sebagai produk dari sinyal kontinu 
ke urutan pulsa persegi panjang yang berulang secara berkala 
– pulsa pengatur waktu (Gbr. 1).
(22)
, periode pengulangan 
:
(23)
. Dalam hal ini, pulsa waktunya tidak berdimensi. Mari kita kembangkan barisan impuls tersebut menjadi deret trigonometri:
(24)
, durasi pulsa perlu diarahkan ke nol: 
. Kami akan menyebut sinyal waktu seperti itu ideal. Dalam hal ini, koefisien ekspansi 
dalam deret Fourier semuanya akan sama dengan 1.
(25)
(26)
:
(27)
sebagai fungsi frekuensi. Periode pengulangannya adalah 
. Istilah bernomor memiliki periode pengulangan terpanjang 
, dan ini, karenanya, akan menjadi periode pengulangan seluruh spektrum. Itu adalah spektrum sinyal diskrit memiliki periode pengulangan yang sama dengan frekuensi kuantisasi
.
. Karena fakta itu 
adalah produk dari fungsi 
Dan 
, spektrum sinyal diskrit 
dihitung sebagai konvolusi spektrum sinyal kontinu 
dan spektrum sinyal waktu 
.
(30)
, menggunakan (25). Karena 
fungsi periodik, spektrumnya diskrit.
.
atau 
- frekuensi melingkar.
atau 
- frekuensi melingkar.
. Grafik fungsi eksponensial yang diteliti disajikan di bawah ini.
Linearitas transformasi Fourier.
Sifat-sifat bagian nyata dan imajiner dari kerapatan spektral.
Kepadatan spektral dari sinyal yang bergeser waktu.
Ketergantungan kerapatan spektral sinyal pada pilihan skala pengukuran waktu.
Kerapatan spektral turunan dan integral tak tentu.
Kepadatan spektral sinyal pada keluaran integrator.
